题目内容
2.在△ABC中,三边分别为a=2,b=3,c=4,求△ABC的面积.分析 先利用余弦定理计算cosB,再利用正弦定理求出sinB,利用S△ABC=$\frac{1}{2}$acsinB,可得结论.
解答 解:∵△ABC中,已知a=2,b=3,c=4,
∴cosB=$\frac{{a}^{2}+{c}^{2}-{b}^{2}}{2ac}$=$\frac{4+9-16}{12}$=-$\frac{1}{4}$,
∴sinB=$\frac{\sqrt{15}}{4}$,
∴S△ABC=$\frac{1}{2}$acsinB=$\frac{3\sqrt{15}}{4}$.
点评 本题主要考查了三角形面积公式、余弦定理在解决三角形问题中的应用,考查了计算能力,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
14.使奇函数f(x)=sin(2x+α)在[-$\frac{π}{4}$,0]上为减函数的α的值可以是( )
| A. | 0 | B. | $\frac{π}{2}$ | C. | π | D. | $\frac{3}{2}$π |
16.在等比数列{an}中,a1=-3,a2=-6,则a4的值为( )
| A. | -24 | B. | 24 | C. | ±24 | D. | -12 |
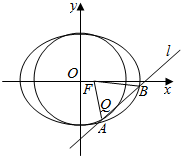 已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )
已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )