题目内容
7.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=6,$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$,则$\overrightarrow a+\overrightarrow b$在$\overrightarrow a$上的投影为5.分析 根据投影的定义便可得到向量$\overrightarrow{a}+\overrightarrow{b}$在$\overrightarrow{a}$上的投影为$|\overrightarrow{a}+\overrightarrow{b}|cos<\overrightarrow{a}+\overrightarrow{b},\overrightarrow{a}>$=$\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}|}$,而根据条件是可以求出$(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}$的,从而便可得出$\overrightarrow{a}+\overrightarrow{b}$在$\overrightarrow{a}$上的投影的值.
解答 解:根据条件,$\overrightarrow{a}+\overrightarrow{b}$在$\overrightarrow{a}$上的投影为:
$|\overrightarrow{a}+\overrightarrow{b}|cos<\overrightarrow{a}+\overrightarrow{b},\overrightarrow{a}>$=$|\overrightarrow{a}+\overrightarrow{b}|\frac{(\overrightarrow{a}+\overrightarrow{b})•\overrightarrow{a}}{|\overrightarrow{a}+\overrightarrow{b}||\overrightarrow{a}|}=\frac{{\overrightarrow{a}}^{2}+\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}|}$=$\frac{{\overrightarrow{a}}^{2}+|\overrightarrow{a}||\overrightarrow{b}|cos\frac{π}{3}}{|\overrightarrow{a}|}=|\overrightarrow{a}|+|\overrightarrow{b}|cos\frac{π}{3}$=$2+6×\frac{1}{2}=5$.
故答案为:5.
点评 考查一个向量在另一个向量方向上的投影的定义,向量夹角的余弦公式,以及向量数量积的计算公式.

 名校课堂系列答案
名校课堂系列答案| A. | 若两条平行直线中的一条平行于这个平面,则另一条也平行于这个平面 | |
| B. | 若直线a不平行于平面α,则α内一定不存在与a平行的直线 | |
| C. | 如果平面α不垂直于平面β,那么平面α内一定不存在直线垂直于平面β | |
| D. | 若三角形ABC在平面α外,则边AB、BC、AC与面α的交点可能不在同一直线上 |
| A. | y=(x-1)2 | B. | f(x)=2-x | C. | y=log0.5(x+1) | D. | $y=\sqrt{x+1}$ |
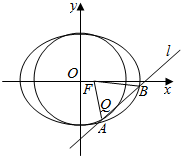 已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )
已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )