题目内容
1.某工厂购买了一套价值200万元的新设备,按每年10%的折旧率折旧,经过7年后价值为原来的50%(用代数式表示,并化简,精确到1年)分析 由设备每年10%的折旧率可得出人口数y(万元)与年份n(年)的函数关系式,由条件列出方程化简后,利用对数的定义、换底公式求出答案.
解答 解:由题意得,一年后,该设备的价值y=200•(1-0.1),
二年后,该设备的价值y=200•(1-0.1)2
n年后,该设备的价值y=200•(1-0.1)n=200×0.9n,(n∈N+),
令200×0.9n=200×50%得,0.9n=$\frac{1}{2}$,
则n=${log}_{0.9}^{\frac{1}{2}}$=$\frac{lg\frac{1}{2}}{lg0.9}$=$\frac{lg1-lg2}{lg0.9}$≈$\frac{0-0.3010}{-0.046}$≈6.543,
所以7年后价值为原来的50%,
故答案为:7.
点评 本题是指数函数的应用题,以及对数的定义、换底公式的应用,列出指数型的关系式是解答的关键,考查计算能力,属于中档题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
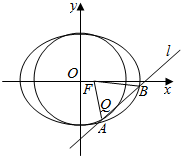 已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )
已知椭圆方程为$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1,点F为右焦点,直线1与圆x2+y2=3相切于点Q,且Q位于y轴的右侧,直线l交椭圆于相异两点A,B,如图所示,则|AF|+|AQ|的值为( )