题目内容
10.如图所示,在多面体P-ABCD中,AB⊥AD,PA⊥平面ABD,PE⊥平面BDE.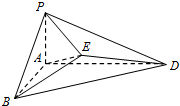
(1)证明:BD⊥平面PAE;
(2)若PA=1,AD=AB=2,PE=$\frac{5}{3}$,求二面角B-PE-A的正切值.
分析 (1)由已知可证PA⊥BD,PE⊥BD.又PE∩PA=P,即可证明BD⊥平面PAE.
(2)取BD中点F,连接EF,AF,由已知及PE垂直于平面BDE,则可求角BEF就是所求二面角,由$\frac{1}{2}AB•AD•AP•\frac{1}{3}$=$\frac{1}{2}BD•EF•PE•\frac{1}{3}$可求EF,从而可求tan∠BEF=$\frac{EF}{BF}$的值.
解答 解:(1)证明:∵PA⊥平面ABD,BD?平面ABD,∴PA⊥BD.
∵PE⊥平面BDE.BD?平面BDE,∴PE⊥BD.
又∵PE∩PA=P,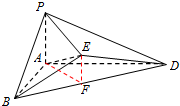
∴BD⊥平面PAE,
(2)如图,取BD中点F,连接EF,AF,
因为PE垂直于平面BDE,则角BEF就是所求二面角,
因为PA=1,AD=AB=2,PE=$\frac{5}{3}$,VP-ABD=VP-BDE,可得:$\frac{1}{2}AB•AD•AP•\frac{1}{3}$=$\frac{1}{2}BD•EF•PE•\frac{1}{3}$,
故有:$\frac{1}{2}×2×2×1×\frac{1}{3}$=$\frac{1}{2}×2\sqrt{2}×EF×\frac{5}{3}×\frac{1}{3}$,解得:EF=$\frac{3\sqrt{2}}{5}$,
所以可得:tan∠BEF=$\frac{EF}{BF}$=$\frac{\frac{3\sqrt{2}}{5}}{\sqrt{2}}$=$\frac{3}{5}$.
点评 本题主要考查了直线与平面垂直的判定,二面角的平面角及求法,考查了空间想象能力和推论论证能力,属于中档题.

练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
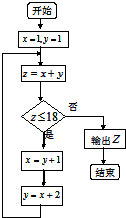
18.阅读如图所示的程序框图,若输出的数据为58,则判断框中应填入的条件为( )


| A. | k≤3 | B. | k≤4 | C. | k≤5 | D. | k≤6 |
5.分配4名水暖工去3个不同的居民家里检查暖气管道,要求4名水暖工都分配出去,并每名水暖工只去一个居民家,且每个居民家都要有人去检查,那么分配的方案共有( )
| A. | $A_4^3$种 | B. | A33A31种 | C. | C41C31种 | D. | C42A33种 |
15.定义在区间[a,b](b>a)上的函数$f(x)=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$的值域是$[-\frac{1}{2},1]$,则b-a的最大值M和最小值m分别是( )
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
20.若$\frac{a}{1-i}$=$\frac{1+i}{i}$(i为虚数单位),则a的值为( )
| A. | i | B. | -i | C. | -2i | D. | 2i |