题目内容
【题目】如图，在四棱锥
中，底面
是直角梯形，
，
，侧面
底面，
，
.
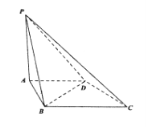
（1）证明：平面
平面
；
（2）若
，求点
到直线
的距离.
【答案】（1）详见解析；（2）
.
【解析】
试题分析：（1）要证明面面垂直，根据判定定理先证明线面垂直，在其中一个平面内找到一条直线与另一个平面垂直，首先做辅助线：延长
交于
点，连接
，根据所给的数字，可得
是
的中点，根据所给的数字，证明
，以及
，可得
平面
，因为
平面
，所以平面
平面；（2）过
点引
于
，
为
到直线
的距离，根据直角三角形等面积转化
，求得
的长度.
试题解析：（1）延长交于点，连接，则
，是的中点，因为
，
所以，又因为侧面
底面
，
，所以
平面
，可得，故平面，因为平面，所以平面平面.
（2）过点引于，为到直线的距离，因为
，
，
，所以
，
，
，
因为，所以
，
所以点
到直线
的距离为
.
【题目】在某次测验中，有6位同学的平均成绩为75分， 用xn表示编号为n（n＝1，2，…，6）的同学所得成绩，且前5位同学的成绩如下：
编号n | 1 | 2 | 3 | 4 | 5 |
成绩xn | 70 | 76 | 72 | 70 | 72 |
（1）求第6位同学的成绩x6，及这6位同学成绩的标准差s；
（2）从前5位同学中选2位同学，求恰有1位同学成绩在区间（68，75）中的概率．
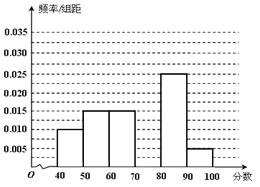
【题目】某学校为了了解学生使用手机的情况，分别在高一和高二两个年级各随机抽取了100名学生进行调查．下面是根据调查结果绘制的学生日均使用手机时间的频数分布表和频率分布直方图，将使用手机时间不低于80分钟的学生称为“手机迷”．
高一学生日均使用手机时间的频数分布表
时间分组 | 频数 |
[0，20） | 12 |
[20，40） | 20 |
[40，60） | 24 |
[60，80） | 18 |
[80，100） | 22 |
[100，120] | 4 |
（1）将频率视为概率，估计哪个年级的学生是“手机迷”的概率大？请说明理由．
（2）在高二的抽查中，已知随机抽到的女生共有55名，其中10名为“手机迷”．根据已知条件完成下面的2×2列联表，并据此资料你有多大的把握认为“手机迷”与性别有关？
非手机迷 | 手机迷 | 合计 | |
男 | |||
女 | |||
合计 |
附：随机变量
（其中
为样本总量）．
参考数据 |
| 0.15 | 0.10 | 0.05 | 0.025 |
| 2.072 | 2.706 | 3.841 | 5.024 |
