Question

【题目】调查表明，高三学生的幸福感与成绩，作业量，人际关系的满意度的指标有极强的相关性，现将这三项的满意度指标分别记为，并对它们进行量化：0表示不满意，1表示基本满意，2表示满意．再用综合指标的值评定高三学生的幸福感等级：若，则幸福感为一级；若，则幸福感为二级；若，则幸福感为三级. 为了了解目前某高三学生群体的幸福感情况，研究人员随机采访了该群体的10名高三学生，得到如下结果：

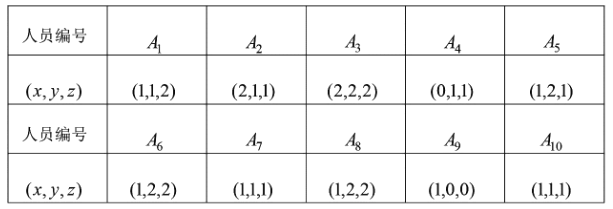
（1）在这10名被采访者中任取两人，求这两人的成绩满意度指标相同的概率；

（2）从幸福感等级是一级的被采访者中任取一人，其综合指标为，从幸福感等级不是一级的被采访者中任取一人，其综合指标为，记随机变量，求的分布列及其数学期望.

Answer 1

【答案】（1）;（2）详见解析.

【解析】

试题分析：（1）首先计算成绩满意指标值相同的人数，分别为0，7,2，所以若10人中任取2人，这2人的成绩满意度指标相同的概率为；（2）是幸福感一级，共有6人，，不是一级的有4人，，所以,例如，包含4-2=2,5-3=2两种情况，a=4的有3人，b=2的有1人，a=5的有2人，b=3的有2人，所以,类似分别计算其他随机变量的概率，得到离散型随机变量的分布列，并计算其数学期望.

试题解析：（1）设事件这10名被采访者中任取两人，这两人的成绩满意度指标相同

成绩满意度指标为0的有：1人

成绩满意度指标为1的有：7人

成绩满意度指标为2的有：2人

则.

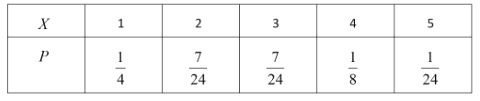
（2）统计结果，幸福感等级是一级的被采访者共6人，幸福感等级不是一级的被采访者共4名，随机变量的所有可能取值为1,2,3,4,5

，，，过程略

.