Question

【题目】已知函数（为常数，），且数列是首项为2，公差为2的等差数列.

（1）若，当时，求数列的前项和；

（2）设，如果中的每一项恒小于它后面的项，求的取值范围．

Answer 1

【答案】（1）；（2）.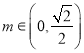

【解析】

试题分析：（1）用等差数列求和公式，结合对数的运算性质可得：，从而有，最后用错位相减法结合等比数列的求和公式，得到数列的前项和；（2）由题意不等式对一切成立，代入的表达式并化简可得．通过讨论单调性可得当时，的最小值是，从而得到，结合，得到实数的取值范围是．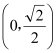

试题解析：（1）由题意，即，

∴，，

当时，，

∴，①

，②

①—②，得，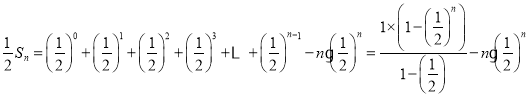

∴．

（2）由（1）知，，要使，对一切成立，

即对一切成立，

∵，∴，∴，对一切恒成立，

只需，

单调递增，∴当时，，∴，且，∴，

综上所述，存在实数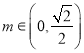满足条件．