题目内容
在极坐标系中, O为极点, 半径为2的圆C的圆心的极坐标为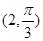 .
.
(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线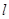 的参数方程为
的参数方程为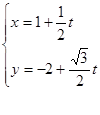 (t为参数),直线
(t为参数),直线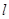 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点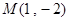 ,求|MA|·|MB|.
,求|MA|·|MB|.
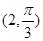 .
.(1)求圆C的极坐标方程;
(2)在以极点O为原点,以极轴为x轴正半轴建立的直角坐标系中,直线
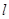 的参数方程为
的参数方程为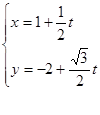 (t为参数),直线
(t为参数),直线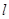 与圆C相交于A,B两点,已知定点
与圆C相交于A,B两点,已知定点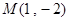 ,求|MA|·|MB|.
,求|MA|·|MB|.(1)  (2)
(2)
 (2)
(2)
试题分析:
(1)把圆心极坐标转化为直角坐标,在直角坐标系里求出圆的方程,再利用极坐标与直角坐标的转化公式,把圆的直角坐标方程转化为极坐标方程,化简即可得到最终结果.
(2)把直线l的参数方程转化为普通方程后,利用联立方程式与韦达定理相结合,采用舍而不求的方式求出|MA|·|MB|的值.
试题解析:(1)由题得,圆心的直角坐标为
 ,所以圆的直角坐标方程为
,所以圆的直角坐标方程为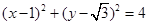 ,再利用极坐标与直角坐标的转化公式可得
,再利用极坐标与直角坐标的转化公式可得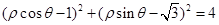 ,化简可得
,化简可得 ,故圆的极坐标方程为
,故圆的极坐标方程为 .
.(2)由题得直线
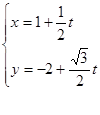 的普通方程为
的普通方程为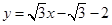 ,设A(
,设A(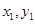 ),B(
),B(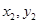 ),联立圆与直线方程得
),联立圆与直线方程得
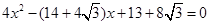
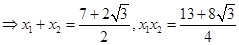 .又|MA|·|MB|
.又|MA|·|MB|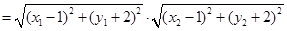
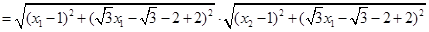
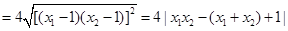


练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
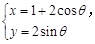 (θ为参数)上,且这两点对应的参数分别为θ=α与θ=2α(0<α<2π),设PQ的中点M与定点A(1,0)间的距离为d,求d的取值范围.
(θ为参数)上,且这两点对应的参数分别为θ=α与θ=2α(0<α<2π),设PQ的中点M与定点A(1,0)间的距离为d,求d的取值范围.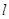 的参数方程为
的参数方程为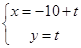 ,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为
,(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,圆C的极坐标方程为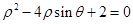 .
.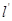 与圆C相切,求h.
与圆C相切,求h. 中,曲线
中,曲线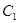 的参数方程为
的参数方程为 (
(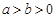 ,
,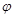 为参数),在以
为参数),在以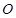 为极点,
为极点,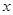 轴的正半轴为极轴的极坐标系中,曲线
轴的正半轴为极轴的极坐标系中,曲线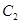 是圆心在极轴上,且经过极点的圆 已知曲线
是圆心在极轴上,且经过极点的圆 已知曲线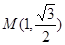 对应的参数
对应的参数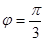 ,射线
,射线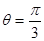 与曲线
与曲线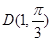
 ,
,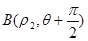 在曲线
在曲线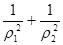 的值
的值 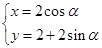 (
(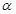 为参数)M是C1上的动点,P点满足
为参数)M是C1上的动点,P点满足 ,P点的轨迹为曲线C2
,P点的轨迹为曲线C2 与C1的异于极点的交点为A,与C2的异于极点的交点为B,求
与C1的异于极点的交点为A,与C2的异于极点的交点为B,求 .
.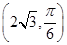 的圆的极坐标方程.
的圆的极坐标方程.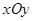 中,曲线
中,曲线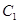 的参数方程为
的参数方程为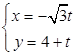 (
(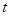 为参数).以
为参数).以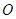 为极点,射线
为极点,射线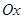 为极轴的极坐标系中,曲线
为极轴的极坐标系中,曲线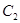 的方程为
的方程为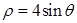 ,曲线
,曲线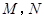 两点,则线段
两点,则线段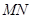 的长度为___________.
的长度为___________.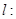
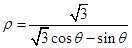 交极轴于
交极轴于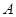 点,过极点
点,过极点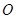 作
作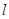 的垂线,垂足为
的垂线,垂足为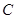 ,现将线段
,现将线段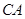 绕极点
绕极点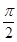 ,则在旋转过程中线段
,则在旋转过程中线段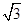 ,0)与曲线C上任意两点的连线所成的最大夹角是
,0)与曲线C上任意两点的连线所成的最大夹角是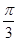 ,则m=________.
,则m=________.