题目内容
在平面直角坐标系xOy中，设动点P，Q都在曲线C：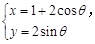
（θ为参数）上，且这两点对应的参数分别为θ＝α与θ＝2α(0＜α＜2π)，设PQ的中点M与定点A(1，0)间的距离为d，求d的取值范围．
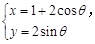（θ为参数）上，且这两点对应的参数分别为θ＝α与θ＝2α(0＜α＜2π)，设PQ的中点M与定点A(1，0)间的距离为d，求d的取值范围．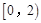
试题分析： 根据题意由所给曲线参数方程，不难得出点P和点Q的坐标，结全中点坐标公式可得中点M的坐标，再利用两点间距离公式即可求出d的表达式，运用三角公式化简可得：
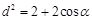，注意所给角的范围，得出d的取值范围．试题解析：由题设可知P ( 1 + 2cosα，2sinα )，Q ( 1 + 2cos2α，sin2α )， 2分
于是PQ的中点M
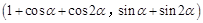． 4分从而
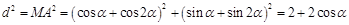6分因为0＜α＜2π，所以－1≤cosα＜1， 8分
于是0≤d 2＜4，故d的取值范围是
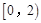． 10分
练习册系列答案
相关题目
．
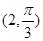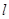的参数方程为
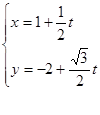（t为参数），直线
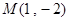,求|MA|·|MB|．
．
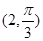的参数方程为
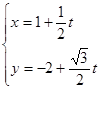（t为参数），直线
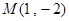,求|MA|·|MB|．
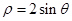的圆与参数方程
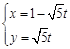的直线的位置关系是 .
(
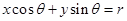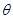是常数)与圆
(
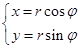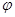是参数)的位置关系是
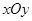中，直线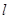
的参数方程为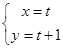
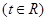，圆C的参数方程为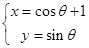
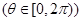，P点在圆C上，则点P到直线
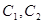的极坐标方程分别为
，
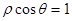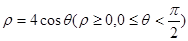则曲线
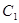与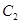
交点的极坐标为 ．
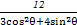,点F1,F2为其左、右焦点,直线l的参数方程为
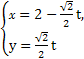(t为参数,t∈R).