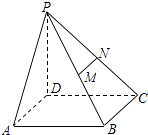
题目内容
【题目】已知椭圆![]() :
: ![]() (
(![]() )的左右焦点分别为
)的左右焦点分别为![]() ,
, ![]() ,离心率为
,离心率为![]() ,点
,点![]() 在椭圆
在椭圆![]() 上,
上, ![]() ,
, ![]() ,过
,过![]() 与坐标轴不垂直的直线
与坐标轴不垂直的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
, ![]() 两点.
两点.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)若![]() ,
, ![]() 的中点为
的中点为![]() ,在线段
,在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求实数
?若存在,求实数![]() 的取值范围;若不存在,说明理由.
的取值范围;若不存在,说明理由.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】【试题分析】(1)依据题设运用余弦定理及已知条件建立方程进行求解;(2)依据题设先建立直线的方程,再运用直线与椭圆的位置关系分析求解:
(Ⅰ)由![]() 得
得![]() ,
, ![]() ,
, ![]() ,
,
由余弦定理得, ![]() ,
,
解得![]() ,
, ![]() ,
, ![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(Ⅱ)存在这样的点![]() 符合题意.
符合题意.
设![]() ,
, ![]() ,
, ![]() ,
,
由![]() ,设直线
,设直线![]() 的方程为
的方程为![]() ,
,
由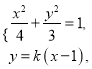 得
得![]() ,
,
由韦达定理得![]() ,故
,故![]() ,
,
又点![]() 在直线
在直线![]() 上,
上, ![]() ,所以
,所以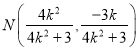 .
.
因为![]() ,所以
,所以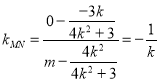 ,整理得
,整理得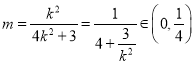 ,
,
所以存在实数![]() ,且
,且![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】甲,乙两台机床同时生产一种零件,其质量按测试指标划分:指标大于或等于95为正品,小于95为次品,现随机抽取这两台车床生产的零件各100件进行检测,检测结果统计如下:
测试指标 |
|
|
|
|
|
机床甲 | 8 | 12 | 40 | 32 | 8 |
机床乙 | 7 | 18 | 40 | 29 | 6 |
(1)试分别估计甲机床、乙机床生产的零件为正品的概率;
(2)甲机床生产一件零件,若是正品可盈利160元,次品则亏损20元;乙机床生产一件零件,若是正品可盈利200元,次品则亏损40元,在(1)的前提下,现需生产这种零件2件,以获得利润的期望值为决策依据,应该如何安排生产最佳?