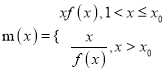题目内容
【题目】已知抛物线
： 
，定点
（常数
）的直线
与曲线
相交于
、
两点.
（1）若点
的坐标为
，求证： 
（2）若
，以
为直径的圆的位置是否恒过一定点？若存在，求出这个定点，若不存在，请说明理由.
【答案】（1）证明见解析（2））以
为直径的圆恒过定点
【解析】试题分析：（1）要证明∠AED=∠BED，根据直线的倾斜角与斜率的关系，只要证KAE=-KBE即可，讨论直线AB的斜率是否存在，设出直线方程，联立抛物线的方程，运用韦达定理和直线的斜率公式，即可得证；（2）设动直线l方程为x=ty+b，表示出B坐标，联立l与抛物线解析式，消去x得到关于y的方程，根据根的判别式等于0得出t与b的关系式，进而设出A与O的坐标，表示出向量AO与向量BO根据圆周角定理得到两向量垂直，即数量积为0，列出关系式，确定出当m=1，n=0时，上式对任意x∈R恒成立，即可得出使得以AB为直径的圆恒过点O，以及此时O的坐标.
试题解析：（1）（a）当直线
垂直于
轴时，根据抛物线的对称性有， 
；
当直线
与
轴不垂直时，依题意，
可设直线
的方程为
（
， 
）
， 
，则
、
两点的坐标
满足方程组
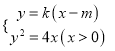消去
并整理，得
， 
设直线
和
的斜率分别为
， 
，则
， 
.
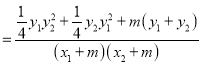
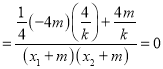
综合（a）（b）可知
.
（2）以
为直径的圆恒过定点
.提示：证明
练习册系列答案
相关题目
