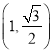题目内容
【题目】已知圆 M与圆N:(x﹣ ![]() )2+(y+
)2+(y+ ![]() )2=r2关于直线y=x对称,且点D(﹣
)2=r2关于直线y=x对称,且点D(﹣ ![]() ,
, ![]() )在圆M上.
)在圆M上.
(1)判断圆M与圆N的公切线的条数;
(2)设P为圆M上任意一点,A(﹣1, ![]() ),B(1,
),B(1, ![]() ),P,A,B三点不共线,PG为∠APB的平分线,且交AB于G,求证:△PBG与△APG的面积之比为定值.
),P,A,B三点不共线,PG为∠APB的平分线,且交AB于G,求证:△PBG与△APG的面积之比为定值.
【答案】
(1)解:由于点N( ![]() ,﹣
,﹣ ![]() )关于直线y=x对称点M(﹣
)关于直线y=x对称点M(﹣ ![]() ,
, ![]() ),
),
r=|ND|= ![]() ,故圆M的方程为:(x+
,故圆M的方程为:(x+ ![]() )2+(y﹣
)2+(y﹣ ![]() )2=
)2= ![]() .
.
根据|MN|= ![]() =
= ![]() >2r,故两圆相离,
>2r,故两圆相离,
∴圆M与圆N的公切线有4条.
(2)证明:设∠PAB=2α,则∠APG=∠BPG=α,∴△PBG与△APG的面积之比= ![]() .
.
设点P(x,y),则:(x+ ![]() )2+(y﹣
)2+(y﹣ ![]() )2=
)2= ![]() .
.
PA2=(x+1)2+(y﹣ ![]() )2 =(x+1)2+
)2 =(x+1)2+ ![]() ﹣(x+
﹣(x+ ![]() )2=﹣
)2=﹣ ![]() x;
x;
PB2=(x﹣1)2+(y﹣ ![]() )2 =(x﹣1)2+
)2 =(x﹣1)2+ ![]() ﹣(x+
﹣(x+ ![]() )2=﹣
)2=﹣ ![]() x;
x;
∴ ![]() =2,即△PBG与△APG的面积之比=2.
=2,即△PBG与△APG的面积之比=2.
【解析】(1)先求得点N关于直线y=x对称点M的坐标,可得圆M的方程,再根据圆心距大于两圆的半径之和,可得两圆相离,即可得出结论;(2)设∠PAB=2α,则∠APG=∠BPG=α,可得△PBG与△APG的面积之比= ![]() .设点P(x,y),求得PA2和 PB2的值,可得
.设点P(x,y),求得PA2和 PB2的值,可得 ![]() 的值,即为△PBG与△APG的面积之比.
的值,即为△PBG与△APG的面积之比.

练习册系列答案
相关题目