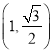题目内容

【题目】已知函数f（x）=ex ， g（x）=ln 的图象分别与直线y=m交于A，B两点，则|AB|的最小值为（ ）
A.2
B.2+ln2
C.e2
D.2e﹣ln

【答案】B
【解析】解：由题意，A（lnm，m），B（2 ，m），其中2 ＞lnm，且m＞0， ∴|AB|=2 ﹣lnm，
令y= ﹣lnx（x＞0），则y′= ﹣ ，
∴x= ，
∴0＜x＜ 时，y′＜0；x＞ 时，y′＞0，
∴y= ﹣lnx（x＞0）在（0， ）上单调递减，在（ ，+∞）上单调递增，
∴x= 时，|AB|min=2+ln2．
故选：B．
由题意，A（lnm，m），B（2 ，m），其中2 ＞lnm，且m＞0，表示|AB|，构造函数，确定函数的单调性，即可求出|AB|的最小值．

练习册系列答案
相关题目

【题目】已知数列{an}满足a1=1，an+1+an= ﹣ ，n∈N* ．
（Ⅰ）求a2 ， a3 ， a4；
（Ⅱ）猜想数列{an}的通项公式，并用数学归纳法证明．

【题目】已知椭圆过点，椭圆的左焦点为，右焦点为，点是椭圆上位于轴上方的动点，且，直线与直线分别交于两点．

（1）求椭圆的方程及线段的长度的最小值；

（2）是椭圆上一点，当线段的长度取得最小值时，求的面积的最大值．

【题目】已知函数f（x）满足f（x﹣1）=﹣f（﹣x+1），且当x≤0时，f（x）=x3 ， 若对任意的x∈[t，t+2]，不等式f（x+t）≥2 f（x）恒成立，则实数t的取值范围是 ．

【题目】设函数f（x）=lnx﹣ax+ ﹣1． （Ⅰ）当a=1时，求曲线f（x）在x=1处的切线方程；
（Ⅱ）当a= 时，求函数f（x）的单调区间；
（Ⅲ）在（Ⅱ）的条件下，设函数g（x）=x2﹣2bx﹣ ，若对于x1∈[1，2]，x2∈[0，1]，使f（x1）≥g（x2）成立，求实数b的取值范围．

【题目】已知函数．

（1）若，求的值；

（2）设为整数，且对于任意正整数， ，求的最小值．

【题目】已知a，b是实数，函数f（x）=x|x﹣a|+b．
（1）当a=2时，求函数f（x）的单调区间；
（2）当a＞0时，求函数f（x）在区间[1，2]上的最大值；
（3）若存在a∈[﹣3，0]，使得函数f（x）在[﹣4，5]上恒有三个零点，求b的取值范围．

【题目】如图，已知复平面内平行四边形ABCD中，点A对应的复数为﹣1， 对应的复数为2+2i， 对应的复数为4﹣4i．
（Ⅰ）求D点对应的复数；
（Ⅱ）求平行四边形ABCD的面积．

【题目】用系统抽样方法从960人中抽取32人做问卷调查为此将他们随机编号为1，2，…，960，分组后在第一组采用简单随机抽样的方法抽到的号码为9，若抽到的32人中，编号落入区间[1，450]的人做问卷A，编号落人区间[451，750]的人做问卷B，其余的人做问卷C，则抽到的人中，做问卷C的人数为 ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网