题目内容
【题目】如图,在棱长为![]() 的正方体
的正方体![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() 和
和![]() 的中点.
的中点.

(![]() )求异面直线
)求异面直线![]() 与
与![]() 所成角的余弦值.
所成角的余弦值.
(![]() )在棱
)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得二面角
,使得二面角![]() 的大小为
的大小为![]() ?若存在,求出
?若存在,求出![]() 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
【答案】(![]() )
)![]() .(
.(![]() )存在,
)存在,![]() .
.
【解析】试题分析:(1)取![]() 中点
中点![]() ,根据平行公理得
,根据平行公理得![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,再根据直角三角形解角,(2)连结
所成角,再根据直角三角形解角,(2)连结![]() ,
,![]() 交于点
交于点![]() ,则根据三垂线定理得
,则根据三垂线定理得![]() 为二面角
为二面角![]() 的平面角,再根据直角三角形解得
的平面角,再根据直角三角形解得![]() .
.
试题解析:(![]() )取
)取![]() 中点
中点![]() ,连结
,连结![]() ,
,
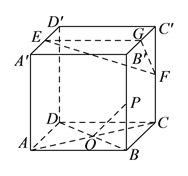
又∵![]() 为
为![]() 中点,
中点,
∴![]() ,
,
连结![]() ,则
,则![]() 即为异面直线
即为异面直线![]() 与
与![]() 所成角,
所成角,
∵![]() 为
为![]() 中点,正方体边长为
中点,正方体边长为![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
故异面直线![]() 与
与![]() 所成角的余弦值为
所成角的余弦值为![]() .
.
(![]() )存在,在棱
)存在,在棱![]() 上取一点
上取一点![]() ,
,
由题意可知,![]() 面
面![]() ,
,
连结![]() ,
,![]() 交于点
交于点![]() ,易知
,易知![]() ,
,![]() ,
,
连结![]() ,则
,则![]() 为二面角
为二面角![]() 的平面角,
的平面角,
当![]() 时,即
时,即![]() ,
,
解得![]() ,
,
∴当![]() 时,二面角
时,二面角![]() 的大小为
的大小为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。