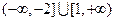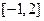题目内容
某企业生产一种产品时,固定成本 为5 000元,而每生产100台产品时直接消耗成本要增加2 500
为5 000元,而每生产100台产品时直接消耗成本要增加2 500 元,市场对此商品年需求量为500台,销售的收入函数为
元,市场对此商品年需求量为500台,销售的收入函数为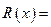
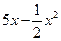 (万元)(0≤
(万元)(0≤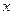 ≤5),其中
≤5),其中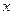 是产品售出的数量(单位:百台)
是产品售出的数量(单位:百台)
(1)把利润表示为年产量的函数;
(2)年产量 多少时,企业所得的利润最大;
多少时,企业所得的利润最大;
(3)年产量多少时,企业才不亏本?
 为5 000元,而每生产100台产品时直接消耗成本要增加2 500
为5 000元,而每生产100台产品时直接消耗成本要增加2 500 元,市场对此商品年需求量为500台,销售的收入函数为
元,市场对此商品年需求量为500台,销售的收入函数为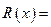
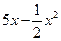 (万元)(0≤
(万元)(0≤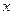 ≤5),其中
≤5),其中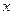 是产品售出的数量(单位:百台)
是产品售出的数量(单位:百台)(1)把利润表示为年产量的函数;
(2)年产量
 多少时,企业所得的利润最大;
多少时,企业所得的利润最大;(3)年产量多少时,企业才不亏本?
(1)
(2)当生产475台时,利润最大.
(3)企业年产量在10台到4 800台之间时,企业不亏本.
(2)当生产475台时,利润最大.
(3)企业年产量在10台到4 800台之间时,企业不亏本.
解:(1)利润y是指生产数量x的产品售出后的总收入R(x)与其总成本C(x)之差,由题意,
当x≤5时,产品能全部售出,当x>5时,只能销售500台,所以
=
(2)在0≤x≤5时,y=-x2+4.75x-0.5,当x=-=4.75百台时,ymax=10.781 25 万元.
当x>5 百台时,y<12-0.25×5=10.75 万元,所以当生产475台时,利润最大.
(3)要使企业不亏本,即要求:或
解得5≥x≥4.75-≈ 0.1 百台或5<x<48 百台,即企业年产量在10台到4 800台之间时,企业不亏本.
0.1 百台或5<x<48 百台,即企业年产量在10台到4 800台之间时,企业不亏本.
当x≤5时,产品能全部售出,当x>5时,只能销售500台,所以
=
(2)在0≤x≤5时,y=-x2+4.75x-0.5,当x=-=4.75百台时,ymax=10.781 25 万元.
当x>5 百台时,y<12-0.25×5=10.75 万元,所以当生产475台时,利润最大.
(3)要使企业不亏本,即要求:或
解得5≥x≥4.75-≈
 0.1 百台或5<x<48 百台,即企业年产量在10台到4 800台之间时,企业不亏本.
0.1 百台或5<x<48 百台,即企业年产量在10台到4 800台之间时,企业不亏本.
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 2分)
2分) 验发现,若按每件
验发现,若按每件 20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.  件)是价格x(元/件)的
件)是价格x(元/件)的 一次函数.
一次函数. 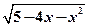 的递增区间是( )
的递增区间是( )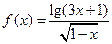 的定义域是 ( )
的定义域是 ( )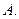
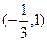
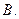
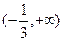 C.
C.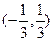 D.
D.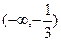
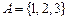 到
到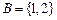 可建立不同的映射的个数为 .
可建立不同的映射的个数为 .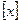 为取
为取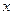 的整数部分,例如:
的整数部分,例如: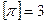 ,
,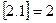 ,
,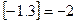 .则方程
.则方程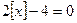 的解集为 ( )
的解集为 ( ) 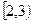 B
B 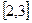 C
C 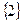 D 2
D 2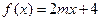 .若在
.若在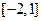 上存在
上存在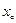 ,使得
,使得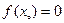 ,则实数
,则实数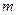 的取值范围是
的取值范围是