题目内容
(本小题满分1 2分)
2分)
某商场购进一批单价为16元的日用品,经试 验发现,若按每件
验发现,若按每件 20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
 2分)
2分)某商场购进一批单价为16元的日用品,经试
 验发现,若按每件
验发现,若按每件 20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数.
20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y(件)是价格x(元/件)的一次函数. (1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
(1) y="-30x+960(16≤x≤32)" (2)当价格为24元时,才能使每月获得最大利润,最大利润为1920元
解:(1)依题意设y=kx+b,
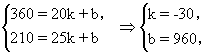
则有:
所以y=-30x+960(16≤x≤32). ………………………………6分
(2)每月获得利润P="(-30x+960)(x-16)"
="30(-x+32)(x-16)"
=30(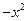 +48x-512
+48x-512 )
)
=-30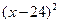 +1920
+1920
所以当x=24时,P有最大值,最大值为1920.
答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.……12分
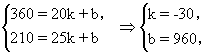
则有:
所以y=-30x+960(16≤x≤32). ………………………………6分
(2)每月获得利润P="(-30x+960)(x-16)"
="30(-x+32)(x-16)"
=30(
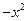 +48x-512
+48x-512 )
) =-30
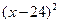 +1920
+1920所以当x=24时,P有最大值,最大值为1920.
答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.……12分

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
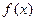 ,若存在x0∈R,使
,若存在x0∈R,使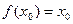 成立,则称x0为
成立,则称x0为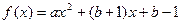 (a≠0)。
(a≠0)。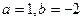 时,求函数
时,求函数 图象上A、B两点的横坐标是函数
图象上A、B两点的横坐标是函数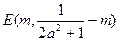 对称,求
对称,求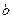 的的最小值。
的的最小值。 为5 000元,而每生产100台产品时直接消耗成本要增加2 500
为5 000元,而每生产100台产品时直接消耗成本要增加2 500 元,市场对此商品年需求量为500台,销售的收入函数为
元,市场对此商品年需求量为500台,销售的收入函数为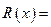
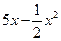 (万元)(0≤
(万元)(0≤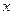 ≤5),其中
≤5),其中 多少时,企业所得的利润最大;
多少时,企业所得的利润最大;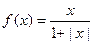 ,下列结论正确的是 。
,下列结论正确的是 。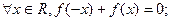
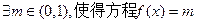 有两个不等的实数解;
有两个不等的实数解;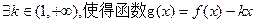 在R上有三个零点;
在R上有三个零点; 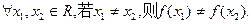
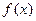 的值域是其定义域的子集,那么
的值域是其定义域的子集,那么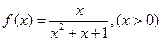 , ②
, ②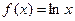
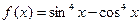
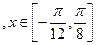 , ④
, ④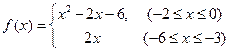
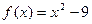 的零点是( )
的零点是( )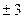
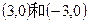
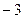
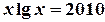 的根,x2是方程
的根,x2是方程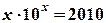 的根,则x1·x2=
的根,则x1·x2=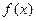 的图象是折线段
的图象是折线段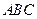 ,其中点
,其中点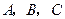 的坐标分别为
的坐标分别为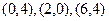 ,则
,则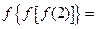 ___.
___.