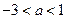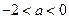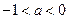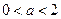题目内容
本小题满分12分)某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y( 件)是价格x(元/件)的
件)是价格x(元/件)的 一次函数.
一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
 件)是价格x(元/件)的
件)是价格x(元/件)的 一次函数.
一次函数. (1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
价格为24元时,才能使每月获得最大利润,最大利润为1920元
解:(1)依题意设y=kx+ b,则有
b,则有
所以y=-30x+960(16≤x≤32).
(2)每月获得利润P="(-30x+960)(x-16)"
="30(-x+32)(x-16)"
=30(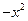 +48x-512)
+48x-512)
=-30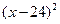 +1920.所以当x=24时,P有最大值,最大值为1920.
+1920.所以当x=24时,P有最大值,最大值为1920.
答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.
 b,则有
b,则有 所以y=-30x+960(16≤x≤32).
(2)每月获得利润P="(-30x+960)(x-16)"
="30(-x+32)(x-16)"
=30(
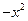 +48x-512)
+48x-512) =-30
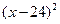 +1920.所以当x=24时,P有最大值,最大值为1920.
+1920.所以当x=24时,P有最大值,最大值为1920. 答:当价格为24元时,才能使每月获得最大利润,最大利润为1920元.

练习册系列答案
相关题目
 为5 000元,而每生产100台产品时直接消耗成本要增加2 500
为5 000元,而每生产100台产品时直接消耗成本要增加2 500 元,市场对此商品年需求量为500台,销售的收入函数为
元,市场对此商品年需求量为500台,销售的收入函数为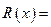
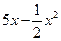 (万元)(0≤
(万元)(0≤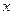 ≤5),其中
≤5),其中 多少时,企业所得的利润最大;
多少时,企业所得的利润最大; 满分14分)已知定义域为R的函数
满分14分)已知定义域为R的函数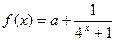 是奇函
是奇函 数.
数.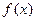 的单调性(不需要写出理由);
的单调性(不需要写出理由);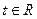 ,不等式
,不等式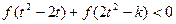 恒成立,求
恒成立,求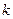 的取值范围.
的取值范围.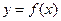 满足:对任意
满足:对任意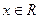 都有
都有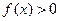 ,且
,且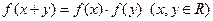
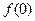 的值;(2)求
的值;(2)求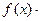
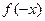 的值;(3)判断函数
的值;(3)判断函数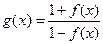 是否具有奇偶性,并证明你的结论。
是否具有奇偶性,并证明你的结论。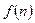 表示处于第
表示处于第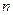 个位置的天干或地
个位置的天干或地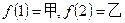 ,
,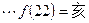 .定义函数
.定义函数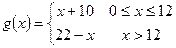 .
.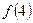 ,
,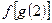 ,
,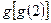
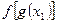
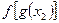 的表示形式来表示该年,求
的表示形式来表示该年,求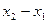
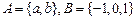 ,从A到B的映射fA→B满足
,从A到B的映射fA→B满足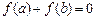 ,那么这样的映射
,那么这样的映射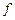 A→B的个数有 ( )
A→B的个数有 ( )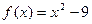 的零点是( )
的零点是( )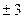
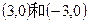
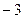
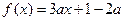 在区间
在区间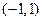 上存在一个零点,则
上存在一个零点,则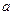 的取值范围是 。
的取值范围是 。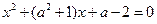 ,有一个根比
,有一个根比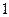 大,另一个根比
大,另一个根比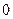 小,
小,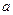 的取值范围是 ( )
的取值范围是 ( )