题目内容
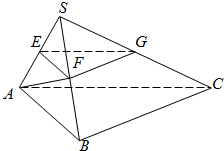
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,求证:
(1)AE∥平面BDF;
(2)平面BDF⊥平面ACE.
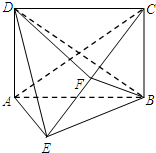
(1)AE∥平面BDF;
(2)平面BDF⊥平面ACE.

证明:(1)设AC∩BD=G,连接FG,易知G是AC的中点,∵F是EC中点,由三角形中位线的性质可得 FG∥AE,
∵AE?平面BFD,FG?平面BFD,∴AE∥平面BFD.
(2)∵平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB∴BC⊥平面ABE,又∵AE?平面ABE,∴BC⊥AE,
又∵AE⊥BE,BC∩BE=B,∴AE⊥平面BCE,∴AE⊥BF.
在△BCE中,BE=CB,F为CE的中点,∴BF⊥CE,AE∩CE=E,∴BF⊥平面ACE,
又BF?平面BDF,∴平面BDF⊥平面ACE.

∵AE?平面BFD,FG?平面BFD,∴AE∥平面BFD.
(2)∵平面ABCD⊥平面ABE,BC⊥AB,
平面ABCD∩平面ABE=AB∴BC⊥平面ABE,又∵AE?平面ABE,∴BC⊥AE,
又∵AE⊥BE,BC∩BE=B,∴AE⊥平面BCE,∴AE⊥BF.
在△BCE中,BE=CB,F为CE的中点,∴BF⊥CE,AE∩CE=E,∴BF⊥平面ACE,
又BF?平面BDF,∴平面BDF⊥平面ACE.

练习册系列答案
相关题目