题目内容
如图,已知四棱锥P-ABCD,底面ABCD为矩形,侧棱PA⊥平面ABCD,其中BC=2AB=2PA=6,M、N为侧棱PC上的两个三等分点.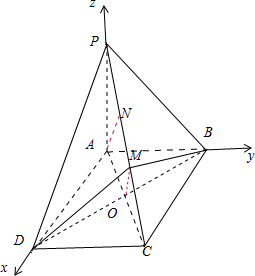
①求证:AN∥平面MBD;
②求二面角M-BD-C的余弦值.

①求证:AN∥平面MBD;
②求二面角M-BD-C的余弦值.
①证明:连接对角线AC交BD于点O,
∵底面ABCD是矩形,∴AO=OC.
又∵NM=MC=
PC,∴OM∥AN.
又∵AN?平面MBD,OM?平面MBD.
∴AN∥平面MBD;
②距离如图所示的空间直角坐标系:∵BC=2AB=2PA=6,∴D(6,0,0),C(6,3,0),B(0,3,0),P(0,0,3).
由M点为线段PC的三等分点,∴M(4,2,1).
∴
=(-6,3,0),
=(-2,2,1).
设平面BMD的法向量
=(x,y,z).
则
即
,令y=2,则x=1,z=
.
∴
=(1,2,
).
∵PA⊥平面BCD,∴可取
=(0,0,3)作为平面BCD的法向量.
∴cos<
,
>=
=
=
.
∴二面角M-BD-C的余弦值为
.

∵底面ABCD是矩形,∴AO=OC.
又∵NM=MC=
| 1 |
| 3 |
又∵AN?平面MBD,OM?平面MBD.
∴AN∥平面MBD;
②距离如图所示的空间直角坐标系:∵BC=2AB=2PA=6,∴D(6,0,0),C(6,3,0),B(0,3,0),P(0,0,3).
由M点为线段PC的三等分点,∴M(4,2,1).
∴
| DB |
| DM |
设平面BMD的法向量
| n |
则
|
|
| 5 |
| 2 |
∴
| n |
| 5 |
| 2 |
∵PA⊥平面BCD,∴可取
| AP |
∴cos<
| n |
| AP |
| ||||
|
|
3×
| ||||||
|
| ||
| 3 |
∴二面角M-BD-C的余弦值为
| ||
| 3 |

练习册系列答案
相关题目