题目内容
【题目】已知椭圆的焦点坐标为F1(﹣1,0),F2(1,0),过F2垂直于长轴的直线交椭圆于P、Q两点,且|PQ|=3.
(1)求椭圆的方程;
(2)过F2的直线l与椭圆交于不同的两点M、N,则△F1MN的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.
【答案】
(1)解:设椭圆方程为 ![]() =1(a>b>0),由焦点坐标可得c=1
=1(a>b>0),由焦点坐标可得c=1
由|PQ|=3,可得 ![]() =3,
=3,
又a2﹣b2=1,解得a=2,b= ![]() ,
,
故椭圆方程为 ![]() =1
=1
(2)解:设M(x1,y1),N(x2,y2),不妨y1>0,y2<0,设△F1MN的内切圆的径R,
则△F1MN的周长=4a=8, ![]() (|MN|+|F1M|+|F1N|)R=4R
(|MN|+|F1M|+|F1N|)R=4R
因此 ![]() 最大,R就最大,
最大,R就最大,
由题知,直线l的斜率不为零,可设直线l的方程为x=my+1,
由 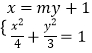 得(3m2+4)y2+6my﹣9=0,
得(3m2+4)y2+6my﹣9=0,
得 ![]() ,
, ![]() ,
,
则 ![]() =
= ![]() ,
,
令t= ![]() ,则t≥1,
,则t≥1,
则 ![]() ,
,
令f(t)=3t+ ![]() ,则f′(t)=3﹣
,则f′(t)=3﹣ ![]() ,
,
当t≥1时,f′(t)≥0,f(t)在[1,+∞)上单调递增,有f(t)≥f(1)=4,S△F1MN≤3,
即当t=1,m=0时,S△F1MN≤3,
S△F1MN=4R,∴Rmax= ![]() ,这时所求内切圆面积的最大值为
,这时所求内切圆面积的最大值为 ![]() π.
π.
故直线l:x=1,△F1MN内切圆面积的最大值为 ![]() π
π
【解析】(1)设椭圆方程,由焦点坐标可得c=1,由|PQ|=3,可得 ![]() =3,又a2﹣b2=1,由此可求椭圆方程;(2)设M(x1 , y1),N(x2 , y2),不妨y1>0,y2<0,设△F1MN的内切圆的径R,则△F1MN的周长=4a=8,
=3,又a2﹣b2=1,由此可求椭圆方程;(2)设M(x1 , y1),N(x2 , y2),不妨y1>0,y2<0,设△F1MN的内切圆的径R,则△F1MN的周长=4a=8, ![]() (|MN|+|F1M|+|F1N|)R=4R,因此
(|MN|+|F1M|+|F1N|)R=4R,因此 ![]() 最大,R就最大.设直线l的方程为x=my+1,与椭圆方程联立,从而可表示△F1MN的面积,利用换元法,借助于导数,即可求得结论.
最大,R就最大.设直线l的方程为x=my+1,与椭圆方程联立,从而可表示△F1MN的面积,利用换元法,借助于导数,即可求得结论.
【考点精析】掌握椭圆的标准方程是解答本题的根本,需要知道椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() .
.


