题目内容
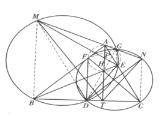
【题目】如图,锐角![]() 的三边互不相等,其垂心为
的三边互不相等,其垂心为![]() ,
,![]() 是边
是边![]() 的中点,直线
的中点,直线![]() ,
,![]() 的外接圆交
的外接圆交![]() 的外接圆于
的外接圆于![]() ,直线
,直线![]() 与
与![]() 的外接圆、
的外接圆、![]() 的外接圆分别交于
的外接圆分别交于![]() 证明:
证明:

(1)![]() 平分
平分![]() ;
;
(2)![]() 三线共点。
三线共点。
【答案】(1)见解析;(2)见解析
【解析】
(1)如图,联结![]() .因
.因![]() 四点共圆,其圆心为
四点共圆,其圆心为![]() ,则
,则![]() .
.
联结![]() .
.
由![]() 和
和![]() 分别四点共圆,得
分别四点共圆,得![]() ,
,
![]() .相加得
.相加得![]() .
.
故![]() 四点共圆.
四点共圆.
又因![]() 四点共圆,即有
四点共圆,即有![]() 五点共圆,此圆直径为
五点共圆,此圆直径为![]() ,设圆心为
,设圆心为![]() .所以,
.所以,![]() ,即
,即![]() 三点共线.
三点共线.
由![]() ,即
,即![]() ,故
,故![]() 为
为![]() 的外接圆直径.从而,
的外接圆直径.从而,![]() .
.
由![]() ,知
,知![]() 为
为![]() 的外接圆直径.进而,
的外接圆直径.进而,![]() ,
,![]() ∥
∥![]() ∥
∥![]() .
.
因直径![]() 过
过![]() 的中点
的中点![]() ,故
,故![]() 垂直且平分弦
垂直且平分弦![]() .
.
同理,![]() 的外接圆直径
的外接圆直径![]() .
.
又![]() ,则
,则![]() ∥
∥![]() ,
,![]() ∥
∥![]() .
.
于是,![]() ∽
∽![]() .所以,
.所以,![]() .①
.①
由![]() ∥
∥![]() ,得
,得![]() ∽
∽![]() .所以,
.所以,![]() .②
.②
①×②,且![]() ,有
,有![]() .
.
所以,![]() ∽
∽![]() .
.
故![]() 平分
平分![]() .
.![]() 平分
平分![]() ;
;
(2)为证![]() 三线共点,只要证
三线共点,只要证![]() 皆过点
皆过点![]() .
.
由于![]() 的圆心角
的圆心角![]() ,
,
所以,![]() ∥
∥![]() .因此,
.因此,![]() 三点共线.
三点共线.
同理,![]() 三点共线.
三点共线.
因此,![]() 三线共点.
三线共点.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目