Question

【题目】如图所示，正四棱锥P﹣ABCD中，侧棱PA与底面ABCD所成的角的正切值为．

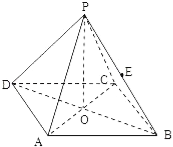
（1）求侧面PAD与底面ABCD所成的二面角的大小；

（2）若E是PB的中点，求异面直线PD与AE所成角的正切值；

（3）问在棱AD上是否存在一点F，使EF⊥侧面PBC，若存在，试确定点F的位置；若不存在，说明理由．

Answer 1

【答案】（1）∠PMO=60°；（2）；（3）F为四等分点

【解析】试题分析：（1）取AD中点M，设PO⊥面ABCD，连MO、PM，则∠PMO为二面角的平面角，设AB=a，则可利用tan∠PAO表示出AO和PO，进而根据求得tan∠PMO的值，则∠PMO可知．

（2）连OE，OE∥PD，∠OEA为异面直线PD与AE所成的角．根据AO⊥BO，AO⊥PO判断出AO⊥平面PBD，进而可推断AO⊥OE，进而可知进而可知∠AEO为直线PD与AE所成角，根据勾股定理求得PD，进而求得OE，则tan∠AEO可求得．

（3）延长MO交BC于N，取PN中点G，连EG、MG．先证出平面PMN和平面PBC垂直，再通过已知条件证出MG⊥平面PBC，取AM中点F，利用EG∥MF，推断出，可知EF∥MG．最后可推断出EF⊥平面PBC．即F为四等分点．

解：（1）取AD中点M，设PO⊥面ABCD，连MO、PM，则∠PMO为二面角的平面角，∠PAO为侧棱PA与底面ABCD所成的角，，

设，PO=AOtan∠PAO=，

∴∠PMO=60°．

（2）连OE，OE∥PD，∠OEA为异面直线PD与AE所成的角．

．

∵

∴

（3）延长MO交BC于N，取PN中点G，连EG、MG．

．

又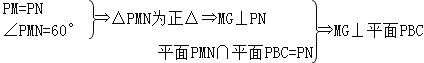

取AM中点F，∵EG∥MF∴

∴EF∥MG．

∴EF⊥平面PBC．

即F为四等分点