题目内容
【题目】已知函数![]() .
.
(1)当![]() ,求函数
,求函数![]() 的极小值;
的极小值;
(2)已知函数![]() 在
在![]() 处取得极值,求证:
处取得极值,求证:![]() ;
;
(3)求函数![]() 的零点个数.
的零点个数.
【答案】(1)![]() ;(2)见解析;(3)见解析;
;(2)见解析;(3)见解析;
【解析】
(1)当![]() 令
令 ![]() ,解得
,解得![]() .即可得出函数
.即可得出函数![]() 的单调性极值点.
的单调性极值点.
(2)![]() ,函数
,函数![]() 在
在![]() 处取得极值,可得
处取得极值,可得![]() ,解得:
,解得:![]() 或
或![]() 时,不满足条件,舍去,因此
时,不满足条件,舍去,因此![]() ,即可证明
,即可证明![]() .
.
(3)![]()
![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ;
;
①![]() ,解得:
,解得:![]() ,此时
,此时![]() 有两个不相等的实数根
有两个不相等的实数根![]() .即函数
.即函数![]() 有两个极值点
有两个极值点![]() .设
.设![]() .对
.对![]() 与
与![]() 与0的大小关系即可得出函数零点的个数.②
与0的大小关系即可得出函数零点的个数.②![]() ,解得:
,解得:![]() 或
或![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上单调递增,即可得出函数
上单调递增,即可得出函数![]() 在
在![]() 上零点的个数.
上零点的个数.
(1)当![]() ,
,![]() .
.
![]() ,
,
令![]() ,解得
,解得![]() ,或
,或![]() ,
,
可得:函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
∴![]() 时函数
时函数![]() 取得极小值,
取得极小值,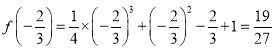 。
。
(2)![]() ,
,
∵函数![]() 在
在![]() 取得极值,
取得极值,
∴![]() ,
,
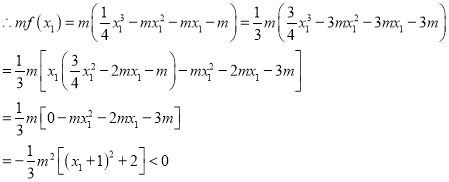
(3)![]() ,
,
![]() ,
,
![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ;
;
①![]() ,解得:
,解得:![]() 或
或![]() ,此时
,此时![]() 有两个不相等的实数根
有两个不相等的实数根![]() .即函数
.即函数![]() 有两个极值点
有两个极值点![]() .设
.设![]() .
.
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上只有一个零点。
上只有一个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上有两个零点。
上有两个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上有三个零点。
上有三个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上有两个零点。
上有两个零点。
![]() 时,可得:函数
时,可得:函数![]() 在
在![]() 上只有一个零点。
上只有一个零点。
②![]() ,解得:
,解得:![]() ,此时
,此时![]() ,函数
,函数![]() 在
在![]() 上单调递增,
上单调递增,![]() 时,
时,![]() ;
; ![]() 时,
时,![]() ;可得:函数
;可得:函数![]() 在
在![]() 上只有一个零点。
上只有一个零点。

练习册系列答案
相关题目