题目内容
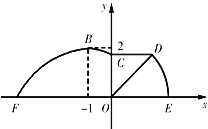
【题目】![]() 是椭圆
是椭圆![]() 的两个焦点,
的两个焦点,![]() 是椭圆
是椭圆![]() 上一点,当
上一点,当![]() 时,有
时,有![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设过椭圆右焦点![]() 的动直线
的动直线![]() 与椭圆交于
与椭圆交于![]() 两点,试问:在
两点,试问:在![]() 铀上是否存在与
铀上是否存在与![]() 不重合的定点
不重合的定点![]() ,使得
,使得![]() 恒成立?
恒成立?
【答案】(1)![]() 1. (2)T(4,0).
1. (2)T(4,0).
【解析】
(1)由题意可得c![]() ,结合椭圆的定义及条件可得
,结合椭圆的定义及条件可得![]() ,解出a,b即可求出椭圆的方程,
,解出a,b即可求出椭圆的方程,
(2)假设存在符合条件的点T,设T(t,0),A(x1,y1),B(x2,y2),由题意可将条件转化为直线AT与BT的斜率之和为0,设直线l的方程为y=k(x﹣2),联立直线与椭圆的方程,利用韦达定理和斜率公式即可求出t=4,当直线l的斜率不存在时,显然满足kAT+kBT=0,即可得解.
(1)由题知,椭圆![]() 的半焦距为c=2,又由椭圆的定义可知
的半焦距为c=2,又由椭圆的定义可知![]() ,即
,即![]() ,∴
,∴![]() ,∴
,∴![]()
∴椭圆的方程为![]() 1.
1.
(2)假设存在符合条件的点T满足![]() ,则x轴为
,则x轴为![]() 的角平分线,即直线AT与BT的斜率之和为0,
的角平分线,即直线AT与BT的斜率之和为0,
设T(t,0),A(x1,y1),B(x2,y2),
设直线l的方程为y=k(x﹣2),
由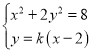 ,
,
可得(2k2+1)x2﹣8k2x+8k2﹣8=0,
∴x1+x2![]() ,x1x2
,x1x2![]() ,
,
由kAT+kBT=0,得![]() 0,
0,
∴![]() 0,
0,
∴2x1x2﹣(t+2)(x1+x2)+4t=0,
解得t=4,
即T(4,0),
当直线l的斜率不存在时,直线l的方程为x=2,
与椭圆的交点坐标分别为(2,![]() ),(2,
),(2,![]() ),显然满足kAT+kBT=0,
),显然满足kAT+kBT=0,
∴存在点T(4,0),满足题意.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目