题目内容
【题目】有一个墙角,两墙面所成二面角的大小为![]() 有一块长为
有一块长为![]() 米,宽为
米,宽为![]() 米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓
米的矩形木板.用该木板档在墙角处,木板边紧贴墙面和地面,和墙角、地面围成一个直角三棱柱储物仓![]() .
.
(1)当![]() 为多少米时,储物仓底面三角形
为多少米时,储物仓底面三角形![]() 面积最大?
面积最大?
(2)当![]() 为多少米时,储物仓的容积最大?
为多少米时,储物仓的容积最大?
(3)求储物仓侧面积的最大值.
【答案】(1)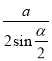 ;(2)
;(2)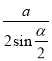 ;(3)
;(3)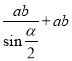
【解析】
(1)设![]() ,讨论
,讨论![]() 和
和![]() 两种情况,利用利用基本不等式得出底面三角形的面积的最大值;
两种情况,利用利用基本不等式得出底面三角形的面积的最大值;
(2)设![]() ,讨论
,讨论![]() 和
和![]() 两种情况,利用利用基本不等式得出三棱柱的体积的最大值;
两种情况,利用利用基本不等式得出三棱柱的体积的最大值;
(3)设![]() ,讨论
,讨论![]() 和
和![]() 两种情况,利用利用基本不等式得三棱柱的侧面积的最大值.
两种情况,利用利用基本不等式得三棱柱的侧面积的最大值.
解:如图所示:

(1)设![]() ,
,
①若![]() ,则
,则![]() ,
,
∴![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∴![]() ,
,
②若![]() ,同理可得
,同理可得![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
又![]() ,故当
,故当![]() ,
,![]() 时,储物仓底面三角形ABC的面积最大,
时,储物仓底面三角形ABC的面积最大,
此时,![]() 为等腰三角形,
为等腰三角形,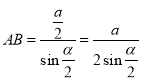 。
。
(2)设![]() ,
,
①若![]() ,由(1)①可知储物仓的容积
,由(1)①可知储物仓的容积![]() ,
,
②若![]() ,由(1)②可知储物仓的容积
,由(1)②可知储物仓的容积![]() ,
,
![]() 又
又 ![]() ,
,
![]() ,
,
由(1)可知当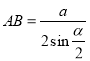 时,储物仓的容积最大.
时,储物仓的容积最大.
(3)设![]() ,
,
①若![]() ,则由余弦定理可得
,则由余弦定理可得![]() ,
,
![]() ,即
,即![]() ,
,
又![]() ,
,
解得:![]() ,当且仅当
,当且仅当![]() 时取等号.
时取等号.
∴储物仓的侧面积为![]() ,
,
②若![]() ,同理可得储物仓的侧面积为
,同理可得储物仓的侧面积为![]() ,
,
综上,储物仓的侧面积的最大值为![]() 。
。

【题目】某电视台为宣传本市,随机对本市内![]() 岁的人群抽取了
岁的人群抽取了![]() 人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
人,回答问题“本市内著名旅游景点有哪些” ,统计结果如图表所示.
组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
第1组 | [15,25) | a | 0.5 |
第2组 | [25,35) | 18 | x |
第3组 | [35,45) | b | 0.9 |
第4组 | [45,55) | 9 | 0.36 |
第5组 | [55,65] | 3 | y |

(1)分别求出![]() 的值;
的值;
(2)根据频率分布直方图估计这组数据的中位数(保留小数点后两位)和平均数;
(3)若第1组回答正确的人员中,有2名女性,其余为男性,现从中随机抽取2人,求至少抽中1名女性的概率.

