题目内容
【题目】已知函数f(x)＝x3＋sin x，x∈(－1，1)，则满足f(a2－1)＋f(a－1)>0的a的取值范围是( )
A. (0，2)B. (1，
)C. (1，2)D. (0，)
【答案】B
【解析】
在区间（﹣1，1）上，由f（﹣x）＝﹣f（x），且f′（x）＞0可知函数f（x）是奇函数且单调递增，由此可求出a的取值范围．
∵函数f（x）＝x3+sinx，x∈（﹣1，1），
则f（﹣x）＝﹣f（x），∴f（x）在区间（﹣1，1）上是奇函数；
又f′（x）＝3x2+cosx＞0，∴f（x）在区间（﹣1，1）上单调递增；
∵f（a2﹣1）+f（a﹣1）＞0，∴﹣f（a﹣1）＜f（a2﹣1），∴f（1﹣a）＜f（a2﹣1），
∴
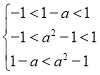，求得1＜a＜
，
故选：B．
练习册系列答案
相关题目
