题目内容
在平面直角坐标系 中,椭圆
中,椭圆 为
为
(1)若一直线与椭圆 交于两不同点
交于两不同点 ,且线段
,且线段 恰以点
恰以点 为中点,求直线
为中点,求直线 的方程;
的方程;
(2)若过点 的直线
的直线 (非
(非 轴)与椭圆
轴)与椭圆 相交于两个不同点
相交于两个不同点 试问在
试问在 轴上是否存在定点
轴上是否存在定点 ,使
,使 恒为定值
恒为定值 ?若存在,求出点
?若存在,求出点 的坐标及实数
的坐标及实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 中,椭圆
中,椭圆 为
为
(1)若一直线与椭圆
 交于两不同点
交于两不同点 ,且线段
,且线段 恰以点
恰以点 为中点,求直线
为中点,求直线 的方程;
的方程;(2)若过点
 的直线
的直线 (非
(非 轴)与椭圆
轴)与椭圆 相交于两个不同点
相交于两个不同点 试问在
试问在 轴上是否存在定点
轴上是否存在定点 ,使
,使 恒为定值
恒为定值 ?若存在,求出点
?若存在,求出点 的坐标及实数
的坐标及实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. (1)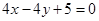 ;(2)在
;(2)在 轴上存在定点
轴上存在定点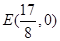 ,使
,使 恒为定值
恒为定值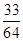 。
。
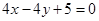 ;(2)在
;(2)在 轴上存在定点
轴上存在定点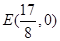 ,使
,使 恒为定值
恒为定值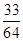 。
。本试题主要是考查了直线与圆的位置关系综合运用。
(1)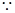 点
点 在椭圆内部,
在椭圆内部,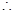 直线
直线 与椭圆必有公共点
与椭圆必有公共点
再利用点差法得到中点坐标与直线斜率的关系式,
(2)假定存在定点 ,使
,使 恒为定值
恒为定值
由于直线 不可能为
不可能为 轴
轴
于是可设直线 的方程为
的方程为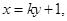 且设点
且设点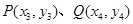
将 代入
代入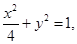 得到一元二次方程,进而利用向量的关系得到参数的值。
得到一元二次方程,进而利用向量的关系得到参数的值。
解:(1)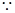 点
点 在椭圆内部,
在椭圆内部, 直线
直线 与椭圆必有公共点
与椭圆必有公共点
设点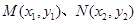 ,由已知
,由已知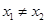 ,则有
,则有
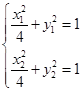 两式相减,得
两式相减,得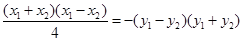
而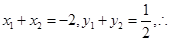 直线
直线 的斜率为
的斜率为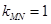
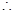 直线
直线 的方程为
的方程为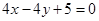
(2) 假定存在定点 ,使
,使 恒为定值
恒为定值
由于直线 不可能为
不可能为 轴
轴
于是可设直线 的方程为
的方程为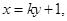 且设点
且设点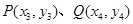
将 代入
代入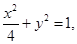 得
得
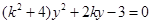 .
.
显然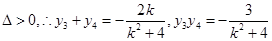
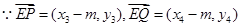 ,
,
则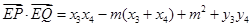

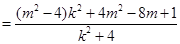
若存在定点 使
使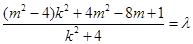 为定值(
为定值( 与
与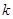 值无关),则必有
值无关),则必有
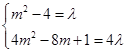
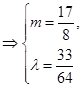
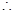 在
在 轴上存在定点
轴上存在定点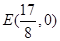 ,使
,使 恒为定值
恒为定值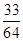
(1)
 点
点 在椭圆内部,
在椭圆内部, 直线
直线 与椭圆必有公共点
与椭圆必有公共点再利用点差法得到中点坐标与直线斜率的关系式,
(2)假定存在定点
 ,使
,使 恒为定值
恒为定值
由于直线
 不可能为
不可能为 轴
轴于是可设直线
 的方程为
的方程为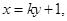 且设点
且设点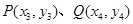
将
 代入
代入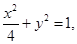 得到一元二次方程,进而利用向量的关系得到参数的值。
得到一元二次方程,进而利用向量的关系得到参数的值。解:(1)
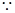 点
点 在椭圆内部,
在椭圆内部,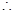 直线
直线 与椭圆必有公共点
与椭圆必有公共点设点
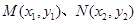 ,由已知
,由已知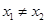 ,则有
,则有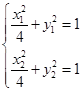 两式相减,得
两式相减,得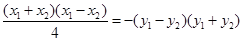
而
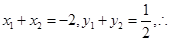 直线
直线 的斜率为
的斜率为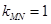
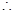 直线
直线 的方程为
的方程为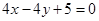
(2) 假定存在定点
 ,使
,使 恒为定值
恒为定值
由于直线
 不可能为
不可能为 轴
轴于是可设直线
 的方程为
的方程为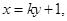 且设点
且设点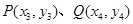
将
 代入
代入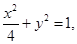 得
得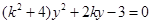 .
.显然
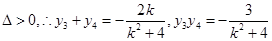
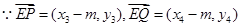 ,
,则
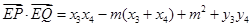

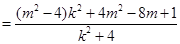
若存在定点
 使
使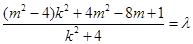 为定值(
为定值( 与
与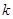 值无关),则必有
值无关),则必有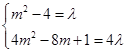
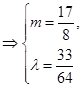
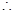 在
在 轴上存在定点
轴上存在定点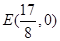 ,使
,使 恒为定值
恒为定值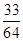

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 ,斜率为
,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,且点
两点,且点 在直线
在直线 轴交点的横坐标
轴交点的横坐标 的取值范围;
的取值范围; 的内切圆的圆心在一条直线上.
的内切圆的圆心在一条直线上. 
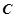 :
: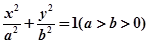 的左、右焦点分别为
的左、右焦点分别为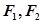 ,上顶点为
,上顶点为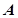 ,过点
,过点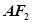 垂直的直线交
垂直的直线交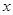 轴负半轴于点
轴负半轴于点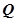 ,且
,且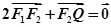 .
.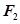 三点的圆恰好与直线
三点的圆恰好与直线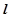 :
: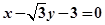 相切,
相切,
 和椭圆
和椭圆 ,则直线和椭圆相交有( )
,则直线和椭圆相交有( )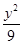 -
-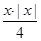 =1交点的个数为___________.
=1交点的个数为___________.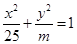 的一个焦点坐标为
的一个焦点坐标为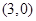 ,那么
,那么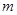 的值为( )
的值为( )



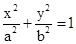 (a>b>0)的离心率为
(a>b>0)的离心率为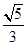 ,短轴一个端点到右焦点的距离为3.
,短轴一个端点到右焦点的距离为3. 与坐标轴正半轴的两个交点.
与坐标轴正半轴的两个交点. 为参数,求椭圆的参数方程;
为参数,求椭圆的参数方程;