题目内容
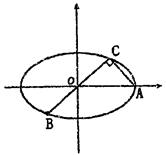
已知A、B、C是椭圆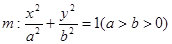 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为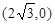 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且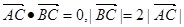
(1)求椭圆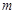 的方程;
的方程;
(2)过点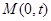 的直线l(斜率存在时)与椭圆m交于两点P,Q,
的直线l(斜率存在时)与椭圆m交于两点P,Q,
设D为椭圆m与y轴负半轴的交点,且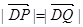 ,求实数t的取值范围.
,求实数t的取值范围.
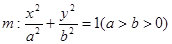 上的三点,其中点A的坐标为
上的三点,其中点A的坐标为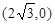 ,BC过椭圆m的中心,且
,BC过椭圆m的中心,且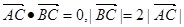

(1)求椭圆
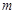 的方程;
的方程;(2)过点
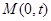 的直线l(斜率存在时)与椭圆m交于两点P,Q,
的直线l(斜率存在时)与椭圆m交于两点P,Q,设D为椭圆m与y轴负半轴的交点,且
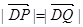 ,求实数t的取值范围.
,求实数t的取值范围.(1)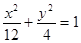 (2)t∈(-2,4)
(2)t∈(-2,4)
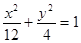 (2)t∈(-2,4)
(2)t∈(-2,4)本题考查椭圆的标准方程,考查直线与椭圆的位置关系,解题的关键是将  转化为kDN•k=-1进行求解.
转化为kDN•k=-1进行求解.
(1)根据椭圆的性质和向量的数量积为零得到a,b的值,得到椭圆的方程。
(2)设出直线与椭圆联立方程组,然后结合根与系数的关系,和向量的等式得到参数的关系式,进而利用判别式得到范围。
解(1)∵ 过(0,0)
过(0,0)
则
∴∠OCA=90°, 即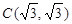 又∵
又∵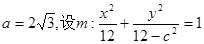
将C点坐标代入得
解得 c2=8,b2=4
∴椭圆m: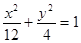
(2)由条件D(0,-2) ∵M(0,t)
1°当k=0时,显然-2<t<2
2°当k≠0时,设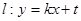
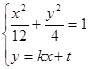 消y得
消y得
由△>0 可得 ①
①
设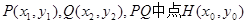
则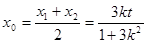

∴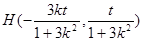
由
∴ ②
②
∴t>1 将①代入②得 1<t<4
∴t的范围是(1,4)
综上t∈(-2,4)
 转化为kDN•k=-1进行求解.
转化为kDN•k=-1进行求解.(1)根据椭圆的性质和向量的数量积为零得到a,b的值,得到椭圆的方程。
(2)设出直线与椭圆联立方程组,然后结合根与系数的关系,和向量的等式得到参数的关系式,进而利用判别式得到范围。
解(1)∵
 过(0,0)
过(0,0)则

∴∠OCA=90°, 即
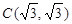 又∵
又∵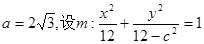
将C点坐标代入得

解得 c2=8,b2=4
∴椭圆m:
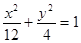
(2)由条件D(0,-2) ∵M(0,t)
1°当k=0时,显然-2<t<2
2°当k≠0时,设
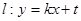
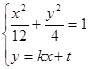 消y得
消y得
由△>0 可得
 ①
①设
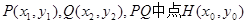
则
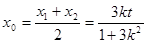

∴
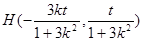
由

∴
 ②
②∴t>1 将①代入②得 1<t<4
∴t的范围是(1,4)
综上t∈(-2,4)

练习册系列答案
相关题目
 的椭圆
的椭圆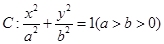 过点
过点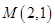 ,
, 为坐标原点,平行于
为坐标原点,平行于 的直线
的直线 交椭圆于
交椭圆于 不同的两点
不同的两点 。
。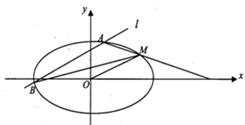
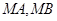 的斜率分别为
的斜率分别为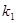 、
、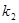 ,求证:
,求证: ,斜率为
,斜率为 的直线
的直线 交椭圆
交椭圆 于
于 两点,且点
两点,且点 在直线
在直线 轴交点的横坐标
轴交点的横坐标 的取值范围;
的取值范围; 的内切圆的圆心在一条直线上.
的内切圆的圆心在一条直线上. 
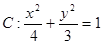 的右顶点是
的右顶点是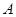 ,上下两个顶点分别为
,上下两个顶点分别为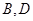 ,四边形
,四边形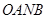 是矩形(
是矩形(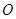 为原点),点
为原点),点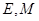 分别为线段
分别为线段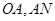 的中点.
的中点.
 与直线
与直线 的交点在椭圆
的交点在椭圆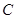 上;
上;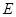 的直线交椭圆于
的直线交椭圆于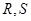 两点,
两点,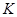 为
为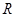 关于
关于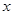 轴的对称点(
轴的对称点(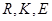 不共线),
不共线),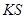 是否经过
是否经过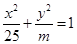 的一个焦点坐标为
的一个焦点坐标为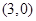 ,那么
,那么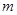 的值为( )
的值为( )



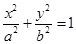 (
(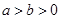 )的左焦点
)的左焦点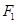 作
作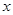 轴的垂线交椭圆于点
轴的垂线交椭圆于点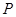 ,
,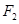 为右焦点,若
为右焦点,若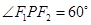 ,则椭圆的离心率为( )
,则椭圆的离心率为( )



 +
+ =1的左、右焦点,c=
=1的左、右焦点,c= ,若直线x=
,若直线x= 上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在点P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )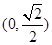



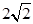 ,相应的焦点
,相应的焦点 的准线了l与x轴相交于A,|OF1|=2|F1A|.
的准线了l与x轴相交于A,|OF1|=2|F1A|. 轴上,且使MF2为
轴上,且使MF2为 的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点;
的一条角平分线,则称点M为椭圆的“左特征点”,求椭圆C的左特征点; 的“左特征点”的位置.
的“左特征点”的位置.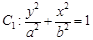
 的右顶点
的右顶点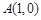 ,过
,过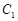 的焦点且垂直长轴的弦长为
的焦点且垂直长轴的弦长为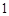 .
.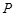 在抛物线
在抛物线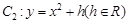 上,
上,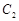 在点
在点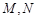 .当线段
.当线段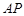 的中点与
的中点与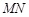 的中点的横坐标相等时,求
的中点的横坐标相等时,求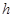 的最小值.
的最小值.