题目内容
19．若函数y=f（x）为定义在R上的奇函数，且在区间（-∞，0]上是减函数，则不等式f（lnx）＜f（1）的解集为（e，+∞）．分析 根据函数奇偶性和单调性之间的关系，将不等式进行转化求解即可．
解答 解：∵y=f（x）为定义在R上的奇函数，且在区间（-∞，0]上是减函数，
∴y=f（x）在R上的为减函数，
则不等式f（lnx）＜f（1）等价为lnx＞1，
即x＞e，
故不等式的解集为（e，+∞），
故答案为：（e，+∞）
点评 本题主要考查不等式的求解，根据函数奇偶性和单调性之间的关系是解决本题的关键．
练习册系列答案
相关题目
9．半期考试结束后学校将安排高二年级到五云山寨社会实践，根据历年气冢统计贸科，五月中旬五云山寨刮大风的概率为0.4，下雨的概率为0.5，既刮大风又下雨的概率为0.3，则在刮大风的条件下下雨的概率为（ ）
| A． | $\frac{2}{5}$ | B． | $\frac{3}{5}$ | C． | $\frac{4}{5}$ | D． | $\frac{3}{4}$ |
在平面直角坐标系xOy中，点A（-1，-2）、B（2，3）、C（-2，-1）．
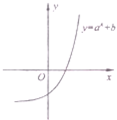函数f（x）=ax+b的图象如图，其中a，b为常数，给出下列四种说法：①a＞1，b＞0；②0＜a＜1，b＜0；③a＞1，b＞-1；④a＞1，b＜-1．则其中所有正确说法的序号是④．
按照如图所示的框图操作，