题目内容
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点,已知函数f(x)=ax2+(b+1)x+b-1(a≠0).
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
(1)当a=1,b=-2时,求f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围.
(1)-1,3(2)0<a<1
(1)当a=1,b=-2时,f(x)=x2-x-3,由题意可知x=x2-x-3,得x1=-1,x2=3,故当a=1,b=-2时,f(x)的不动点是-1,3.
(2)∵f(x)=ax2+(b+1)x+b-1(a≠0)恒有两个不动点,∴x=ax2+(b+1)x+b-1,即ax2+bx+b-1=0恒有两相异实根,∴Δ=b2-4ab+4a>0(b∈R)恒成立.于是Δ′=(4a)2-16a<0,解得0<a<1,故当b∈R,f(x)恒有两个相异的不动点时,0<a<1
(2)∵f(x)=ax2+(b+1)x+b-1(a≠0)恒有两个不动点,∴x=ax2+(b+1)x+b-1,即ax2+bx+b-1=0恒有两相异实根,∴Δ=b2-4ab+4a>0(b∈R)恒成立.于是Δ′=(4a)2-16a<0,解得0<a<1,故当b∈R,f(x)恒有两个相异的不动点时,0<a<1

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 .
. ,
, ,
, ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点; ,若对任意
,若对任意 、
、 ,有
,有 ,求
,求 的取值范围.
的取值范围.

 ,x∈[-1,8],函数g(x)=ax+2,x∈[-1,8],若存在x∈[-1,8],使f(x)=g(x)成立,则实数a的取值范围是________.
,x∈[-1,8],函数g(x)=ax+2,x∈[-1,8],若存在x∈[-1,8],使f(x)=g(x)成立,则实数a的取值范围是________.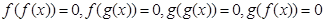 的实根个数分别为a,b,c,d,则a+b+c+d=( )
的实根个数分别为a,b,c,d,则a+b+c+d=( )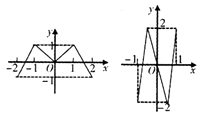
 .当燃料质量是火箭质量的________倍时,火箭的最大速度可以达到12km/s.
.当燃料质量是火箭质量的________倍时,火箭的最大速度可以达到12km/s.