题目内容
设函数 .
.
(1)设 ,
, ,
, ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点;
(2)设 ,若对任意
,若对任意 、
、 ,有
,有 ,求
,求 的取值范围.
的取值范围.
 .
.(1)设
 ,
, ,
, ,证明:
,证明: 在区间
在区间 内存在唯一的零点;
内存在唯一的零点;(2)设
 ,若对任意
,若对任意 、
、 ,有
,有 ,求
,求 的取值范围.
的取值范围.(1)详见解析;(2)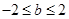 .
.
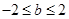 .
.试题分析:(1)利用零点存在定理说明
 在区间
在区间 内存在零点,然后利用函数
内存在零点,然后利用函数 的单调性来说明零点的唯一性;(2)先确定函数
的单调性来说明零点的唯一性;(2)先确定函数 的解析式,将问题等价转化为“
的解析式,将问题等价转化为“ 在
在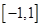 上的最大值与最小值之差
上的最大值与最小值之差 ”,对二次函数
”,对二次函数 的对称轴与区间
的对称轴与区间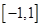 的位置关系来进行分类讨论,从而求解出实数
的位置关系来进行分类讨论,从而求解出实数 的取值范围.
的取值范围.试题解析:(1)当
 ,
, ,
, 时,
时, ,
,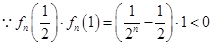 ,
, 在区间
在区间 内存在零点,
内存在零点,又当
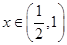 时,
时,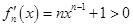 ,
, 在区间
在区间 是单调递增的,
是单调递增的, 在区间
在区间 内存在唯一的零点;
内存在唯一的零点;(2)当
 时,
时,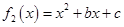 ,
,对任意
 、
、 都有
都有 等价于
等价于 在
在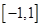 上的最大值与最小值之差
上的最大值与最小值之差 ,
,据此分类讨论如下:
(i)当
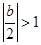 时,即
时,即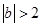 时,
时, ,与题设矛盾!
,与题设矛盾!(ii)当
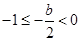 ,即
,即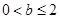 时,
时,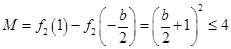 恒成立;
恒成立;(iii)当
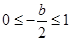 ,即
,即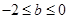 时,
时, .
.综上所述,
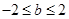 .
.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


 (单位:天)变化的函数关系式近似为
(单位:天)变化的函数关系式近似为 若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用.
若多次喷洒,则某一时刻空气中的净化剂浓度为每次投放的净化剂在相应时刻所释放的浓度之和.由实验知,当空气中净化剂的浓度不低于4(毫克/立方米)时,它才能起到净化空气的作用. )个单位的药剂,要使接下来的4天中能够持续有效净化,试求
)个单位的药剂,要使接下来的4天中能够持续有效净化,试求 的最小值(精确到0.1,参考数据:
的最小值(精确到0.1,参考数据: 取1.4).
取1.4).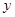 (万元)可以看成月产量
(万元)可以看成月产量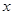 (吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元.
(吨)的二次函数.当月产量为10吨时,月总成本为20万元;当月产量为15吨时,月总成本最低为17.5万元. 的图象关于坐标原点对称。
的图象关于坐标原点对称。 的值,并求出函数
的值,并求出函数 的零点;
的零点; 在[0,1]内存在零点,求实数b的取值范围;
在[0,1]内存在零点,求实数b的取值范围; ,已知
,已知 的反函数
的反函数 =
= ,若不等式
,若不等式 在
在 上恒成立,求满足条件的最小整数k的值。
上恒成立,求满足条件的最小整数k的值。 的定义域为
的定义域为 ,值域也为
,值域也为 为“保域函数”,下列函数是“保域函数”的有 .(填上所有正确答案的序号)
为“保域函数”,下列函数是“保域函数”的有 .(填上所有正确答案的序号) ; ②
; ② ;
; ;④
;④ ;
; 。
。 的解集为空集,则实数m的取值范围是 .
的解集为空集,则实数m的取值范围是 .