题目内容
10.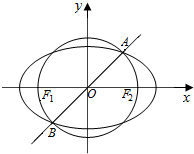 知点F1(-1,0)和点F2(1,0),以F1、F2为焦点的椭圆和以线段F1F2为直径的圆于第一、三象限交于A,B两点,直线AB的斜率为k,若0<k≤$\sqrt{3}$,则此椭圆的离心率e的取值范围为[$\sqrt{3}$-1,1).
知点F1(-1,0)和点F2(1,0),以F1、F2为焦点的椭圆和以线段F1F2为直径的圆于第一、三象限交于A,B两点,直线AB的斜率为k,若0<k≤$\sqrt{3}$,则此椭圆的离心率e的取值范围为[$\sqrt{3}$-1,1).
分析 设出椭圆方程和圆方程,联立求得A,B的交点,运用直线的斜率公式,结合离心率公式和不等式的解法,即可得到所求离心率的范围.
解答 解:设椭圆方程为$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1,
与x2+y2=1联立,可得
x=±$\sqrt{\frac{{a}^{2}{b}^{2}-{a}^{2}}{{b}^{2}-{a}^{2}}}$,y=±$\sqrt{\frac{{b}^{2}-{a}^{2}{b}^{2}}{{b}^{2}-{a}^{2}}}$,
即有直线AB的斜率为k=$\sqrt{\frac{{b}^{2}-{a}^{2}{b}^{2}}{{a}^{2}{b}^{2}-{a}^{2}}}$,
由b2=a2-1,可得k=$\sqrt{\frac{({a}^{2}-1)^{2}}{{a}^{2}(2-{a}^{2})}}$,
由0<k≤$\sqrt{3}$,可得a2(2-a2)>0,且(a2-1)2≤3a2(2-a2),
解得1-$\frac{\sqrt{3}}{2}$≤a2≤1+$\frac{\sqrt{3}}{2}$,
即有$\frac{\sqrt{3}-1}{2}$≤a≤$\frac{\sqrt{3}+1}{2}$,
即有e=$\frac{c}{a}$=$\frac{1}{a}$∈[$\sqrt{3}$-1,$\sqrt{3}$+1].
由0<e<1,可得离心率e的取值范围是[$\sqrt{3}$-1,1).
故答案为:[$\sqrt{3}$-1,1).
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,联立圆的方程和椭圆方程求交点是解题的关键.

练习册系列答案
相关题目
20.已知椭圆$\frac{x^2}{25}$+$\frac{y^2}{16}$=1内有两点A(1,3),B(3,0),P为椭圆上一点,则|PA|+|PB|的最大值为( )
| A. | 10 | B. | 15 | C. | 4 | D. | 5 |
1.已知数列{an}是等差数列,其前n项和为Sn,且a1=1,S5=25,则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前10项和等于( )
| A. | $\frac{9}{19}$ | B. | $\frac{10}{21}$ | C. | $\frac{18}{19}$ | D. | $\frac{20}{21}$ |
5.sin600°=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
15.已知tanα=2,则sin2α的值为( )
| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
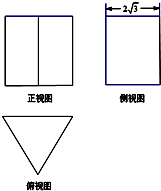 一个体积为16$\sqrt{3}$的正三棱柱(即底面为正三角形,侧棱垂直底面)的三视图如图所示,则这个三棱柱的左视图的面积为8$\sqrt{3}$.
一个体积为16$\sqrt{3}$的正三棱柱(即底面为正三角形,侧棱垂直底面)的三视图如图所示,则这个三棱柱的左视图的面积为8$\sqrt{3}$.