题目内容
1．已知数列{an}是等差数列，其前n项和为Sn，且a1=1，S5=25，则数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前10项和等于（ ）| A． | $\frac{9}{19}$ | B． | $\frac{10}{21}$ | C． | $\frac{18}{19}$ | D． | $\frac{20}{21}$ |
分析 利用等差数列的通项公式及其前n项和公式、“裂项求和”即可得出．
解答 解：设等差数列{an}的公差为d，∵a1=1，S5=25，
∴5×1+$\frac{5×4}{2}d$=25，解得d=2．
∴an=1+2（n-1）=2n-1．
∴$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{（2n-1）（2n+1）}$=$\frac{1}{2}（\frac{1}{2n-1}-\frac{1}{2n+1}）$．
∴数列$\left\{{\frac{1}{{{a_n}{a_{n+1}}}}}\right\}$的前10项和=$\frac{1}{2}[（1-\frac{1}{3}）+（\frac{1}{3}-\frac{1}{5}）$+…+$（\frac{1}{19}-\frac{1}{21}）]$=$\frac{1}{2}（1-\frac{1}{21}）$=$\frac{10}{21}$．
故选：B．
点评 本题考查了等差数列的通项公式及其前n项和公式、“裂项求和”方法，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
12．已知a＞b，则下列不等式中成立的是（ ）
| A． | a2＞b2 | B． | ac＞bc | C． | |a|＞|b| | D． | 2a＞2b |
9．已知a＞b≥2，现有下列不等式：
①b2＜3b-a；②a3+b3＞a2b+ab2；③ab＞a+b；④$\frac{1}{2}$+$\frac{2}{ab}$＞$\frac{1}{a}$+$\frac{1}{b}$．
其中正确的是（ ）
①b2＜3b-a；②a3+b3＞a2b+ab2；③ab＞a+b；④$\frac{1}{2}$+$\frac{2}{ab}$＞$\frac{1}{a}$+$\frac{1}{b}$．
其中正确的是（ ）
| A． | ②④ | B． | ①④ | C． | ②③ | D． | ①③ |
13．圆C1：（x+1）2+（y+2）2=9与圆C2：（x-2）2+（y-2）2=4的位置关系为（ ）
| A． | 相交 | B． | 内切 | C． | 外切 | D． | 外离 |
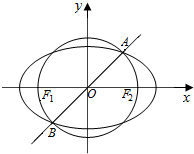知点F1（-1，0）和点F2（1，0），以F1、F2为焦点的椭圆和以线段F1F2为直径的圆于第一、三象限交于A，B两点，直线AB的斜率为k，若0＜k≤$\sqrt{3}$，则此椭圆的离心率e的取值范围为[$\sqrt{3}$-1，1）．