题目内容
11.设A(-3,0),B(3,0)为两定点,动点P到A点的距离与到B点的距离之比为1:2,则点P的轨迹图形所围成的面积是16π.分析 设P点的坐标为(x,y),利用两点间的距离公式代入等式2|PA|=|PB|,化简整理得(x-5)2+y2=16,所以点P的轨迹是一个圆,求出圆的半径利用圆面积公式,即可算出所求图形的面积.
解答 解:设P点的坐标为(x,y),
∵A(-3,0),B(3,0),动点P到A点的距离与到B点的距离之比为1:2,
∴$\sqrt{(x-3)^{2}+{y}^{2}}$=2$\sqrt{(x+3)^{2}+{y}^{2}}$,平方得(x-3)2+y2=4[(x+3)2+y2],
化简得(x+5)2+y2=16,
∴点的轨迹是以(-5,0)为圆心、4为半径的圆,
因此,点P的轨迹所包围的图形的面积S=π•42=16π.
故答案为:16π.
点评 本题给出动点P满足2|PA|=|PB|,求动点的轨迹方程、轨迹所包围的图形的面积.着重考查了两点间的距离公式、圆的标准方程、圆的面积公式和动点轨迹的求法等知识,属于中档题.

练习册系列答案
相关题目
7.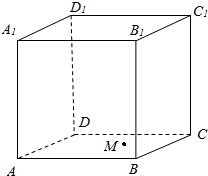 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
 如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )
如图所示,正方体ABCD-A1B1C1D1的棱长为a,平面AC上一动点M到直线AD的距离与到直线D1C1的距离相等,则点M的轨迹为( )| A. | 直线 | B. | 椭圆 | C. | 抛物线 | D. | 双曲线 |
 如图所示,已知正方体ABCD-A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,求EF和CD所成的角.
如图所示,已知正方体ABCD-A1B1C1D1,E、F分别是正方形A1B1C1D1和ADD1A1的中心,求EF和CD所成的角.