题目内容
2.设函数f(x)=logax(a>0,且a≠1)满足f(27)=3,则f-1(log92)的值是$\sqrt{2}$.分析 先求a,再求反函数,然后求出f-1(log92)的值.
解答 解:∵f(27)=3,∴loga27=3,解得a=3,
∴f(x)=log3x,
∴f-1(x)=3x,
所以f-1(log92)=3${\;}^{lo{g}_{9}2}$=3${\;}^{lo{g}_{3}\sqrt{2}}$=$\sqrt{2}$,
故答案为:$\sqrt{2}$.
点评 本题考查了待定系数法求解析式,同底的指数函数与对数函数互为反函数及对数运算,是基础题.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
14.直线$\sqrt{3}$x-y-3=0的倾斜角是( )
| A. | $\frac{π}{3}$ | B. | $\frac{2}{3}$π | C. | $\frac{π}{6}$ | D. | $\frac{4}{3}$π |
16.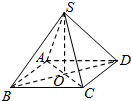 如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )
如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )
 如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )
如图,已知四棱锥S-ABCD的侧棱与底面边长都是2,且底面ABCD是正方形,则侧棱与底面所成的角( )| A. | 75° | B. | 60° | C. | 45° | D. | 30° |