题目内容
【题目】在直角坐标系xOy中，直线l的参数方程是 
（t为参数）．在以坐标原点为极点，x轴正半轴为极轴的极坐标系中，曲线C的极坐标方程为ρ2+12ρcosθ+11=0． （Ⅰ）说明C是哪种曲线？并将C的方程化为直角坐标方程；
（Ⅱ）直线l与C交于A，B两点，|AB|= 
，求l的斜率．
【答案】解：（Ⅰ）由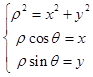 
，得曲线C的直角坐标方程为x2+y2+12x+11=0 即（x+6）2+y2=25，曲线C是以（﹣6，0）为圆心，5为半径的圆
，
（Ⅱ）易得直线l的极坐标方程为θ=α（ρ∈R），
设A，B的极径分别为ρ1 ， ρ2 ， 其是ρ2+12ρcosθ+11=0的解，
于是ρ1+ρ2=﹣12cosα，ρ1ρ2=11， 
，
由 
，得 
， 
，
所以l的斜率为 
或 
．
【解析】（Ⅰ）由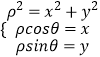 
，得曲线C的直角坐标方程为x2+y2+12x+11=0，即可得出结论；（Ⅱ） 
，由 
，得 
， 
，即可求l的斜率．
练习册系列答案
步步高达标卷系列答案
相关题目
