题目内容
【题目】定义域为R的偶函数f(x)满足x∈R,有f(x+2)=f(x)﹣f(1),且当x∈[2,3]时,f(x)=﹣2x2+12x﹣18,若函数y=f(x)﹣loga(x+1)恰有三个零点,则a的取值范围是( )
A.(0, ![]() )
)
B.(0, ![]() )
)
C.( ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() )
)
【答案】C
【解析】解:∵f(x+2)=f(x)﹣f(1), 且f(x)是定义域为R的偶函数,
令x=﹣1可得f(﹣1+2)=f(﹣1)﹣f(1),
又f(﹣1)=f(1),
可得f(1)=0 则有,f(x+2)=f(x),
∴f(x)是周期为2的偶函数.
当x∈[2,3]时,f(x)=﹣2x2+12x﹣18=﹣2(x﹣3)2 ,
函数f(x)的图象为开口向下、顶点为(3,0)的抛物线.
函数y=f(x)﹣loga(x+1)在(0,+∞)上恰有三个零点,
令g(x)=loga(x+1),则f(x)的图象和g(x)的图象恰有3个交点.
作出函数的图象,如图所示,
∵f(x)≤0,∴g(x)≤0,可得0<a<1.
要使函数y=f(x)﹣loga(|x|+1)在(0,+∞)上恰有三个零点,
则有g(2)>f(2)且f(4)>g(4),即 loga(2+1)>f(2)=﹣2,且﹣2>loga(4+1),
解得 ![]() <a<
<a< ![]() .
.
故选:C.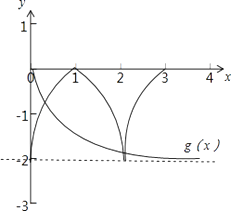

 阅读快车系列答案
阅读快车系列答案【题目】自贡某个工厂于2016年下半年对生产工艺进行了改造(每半年为一个生产周期),从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本,用茎叶图表示如图所示,已知每个生产周期内与其中位数误差在±5范围内(含±5)的产品为优质品,与中位数误差在±15范围内(含±15)的产品为合格品(不包括优质品),与中位数误差超过±15的产品为次品.企业生产一件优质品可获利润20元,生产一件合格品可获利润10元,生产一件次品要亏损10元. 
(Ⅰ)求该企业2016年一年生产一件产品的利润的分布列和期望;
(Ⅱ)是否有95%的把握认为“优质品与生产工艺改造有关”.
附:
P(K2≥k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
K2= ![]() .
.