题目内容
【题目】已知长方体ABCD-A1B1C1D1中,底面ABCD为正方形,AB=4,AA1=2,点E1在棱C1D1上,且D1E1=3。
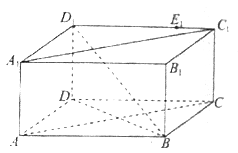
(I)在棱CD上确定一点E,使得直线EE1∥平面D1DB,并写出证明过程;
(II)求证:平面A1ACC1⊥平面D1DB;
(III)若动点F在正方形ABCD内,且AF=2,请说明点F的轨迹,试求E1F长度的最小值。
【答案】(1)DE=3,见解析(2)见解析(3) ![]()
【解析】
试题(1)在DC上取点E,使DE=3,根据平几知识可得DEE1D1为平行四边形,即得EE1∥DD1.再根据线面平行判定定理得结论,(2)先根据长方体性质得AA1⊥DB.再结合正方形性质得AC⊥DB,根据线面垂直判定定理得DB⊥平面A1ACC1.,最后根据面面垂直判定定理得结论,(3)由圆的定义可得点F的轨迹,注意轨迹范围,根据勾股定理得E1F取最小值时EF取最小值.再根据圆的性质求最值.
试题解析:证明:(I)在DC上取点E,使DE=3,此时直线EE1∥平面D1DB.
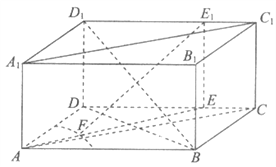
证明如下:在长方体ABCD-A1B1C1D1中,DE∥D1E1,且DE=D1E1,
所以四边形DEE1D1为平行四边形.
所以EE1∥DD1.
又DD1![]() 平面D1DB,EE1
平面D1DB,EE1![]() 平面D1DB,
平面D1DB,
所以直线EE1∥平面D1DB.
(Ⅱ)在正方形ABCD中,AC⊥DB,
又AA1⊥底面ABCD,DB![]() 底面ABCD,
底面ABCD,
所以AA1⊥DB.
又AA1![]() AC=A,
AC=A,
所以DB⊥平面A1ACC1.
又DB![]() 平面D1DB,
平面D1DB,
所以平面A1ACC1⊥平面D1DB.
(III)因为动点F在正方形内,且AF=2,
所以点F的轨迹为以A为圆心,2为半径,在正方形ABCD内的![]() 个圆周。
个圆周。
由题意知,直线EE1⊥平面ABCD,所以EE1⊥EF,故E1F取最小值,即EF取最小值.
所以当A,F,E三点共线时,EF长度最小,即E1F长度最小,
此时AE=![]() ,
,
E1F=![]() .
.
所以E1F的最小值为![]() .
.

【题目】学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?


