题目内容
【题目】如图,△ABC内接于☉O,AB=AC,直线MN切☉O于点C,弦BD∥MN,AC与BD相交于点E. 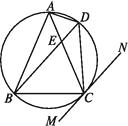
(1)求证:△ABE≌△ACD;
(2)求证:BE=BC.
【答案】
(1)证明:∵BD∥MN,∴∠CDB=∠DCN.
又∠BAE=∠CDB,
∴∠BAE=∠DCN.
又直线MN是☉O的切线,
∴∠DCN=∠CAD.
∴∠BAE=∠CAD.
又∠ABE=∠ACD,AB=AC,
∴△ABE≌△ACD.
(2)证明:∵∠EBC=∠BCM,∠BCM=∠BDC,
∴∠EBC=∠BDC.
∴CB=CD.
∵∠BEC=∠EDC+∠ECD,∠ECD=∠ABE,
∴∠BEC=∠EBC+∠ABE=∠ABC.
又AB=AC,
∴∠ABC=∠ECB.
∴∠BEC=∠ECB.
∴BE=BC.
【解析】本题主要考查了弦切角的性质,解决问题的关键是根据弦切角的性质(1)由已知,得∠ABE=∠ACD,只需证明∠BAE=∠CAD,转化为证明∠BAE=∠CDB,∠CDB=∠DCN,∠DCN=∠CAD.(2)转化为证明∠BEC=∠ECB.

练习册系列答案
相关题目