题目内容
设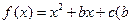 、
、 .
.
(1)若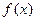 在
在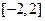 上不单调,求
上不单调,求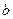 的取值范围;
的取值范围;
(2)若 对一切
对一切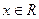 恒成立,求证:
恒成立,求证: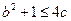 ;
;
(3)若对一切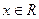 ,有
,有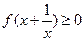 ,且
,且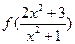 的最大值为1,求
的最大值为1,求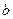 、
、 满足的条件.
满足的条件.
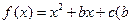 、
、 .
.(1)若
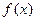 在
在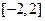 上不单调,求
上不单调,求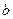 的取值范围;
的取值范围;(2)若
 对一切
对一切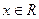 恒成立,求证:
恒成立,求证: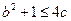 ;
;(3)若对一切
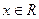 ,有
,有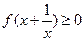 ,且
,且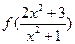 的最大值为1,求
的最大值为1,求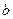 、
、 满足的条件.
满足的条件.(1)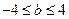
(2)证明见解析。
(3)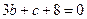 且
且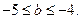
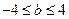
(2)证明见解析。
(3)
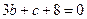 且
且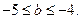
(1)由题意 ,
,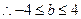 ;
;
(2)须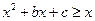 与
与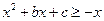 同时成立,即
同时成立,即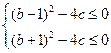 ,
,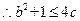 ;
;
(3)因为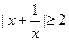 ,依题意,对一切满足
,依题意,对一切满足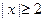 的实数
的实数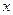 ,有
,有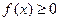 .
.
①当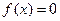 有实根时,
有实根时,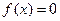 的实根在区间
的实根在区间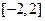 内,设
内,设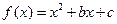 ,所以
,所以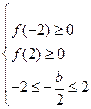 ,即
,即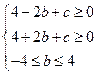 ,又
,又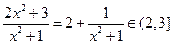 ,于是,
,于是,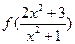 的最大值为
的最大值为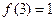 ,即
,即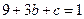 ,从而
,从而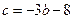 .故
.故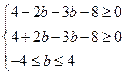 ,即
,即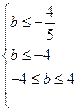 ,解得
,解得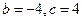 .
.
②当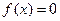 无实根时,
无实根时,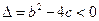 ,由二次函数性质知,
,由二次函数性质知,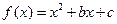 在
在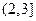 上的最大值只能在区间的端点处取得,所以,当
上的最大值只能在区间的端点处取得,所以,当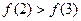 时,
时,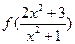 无最大值.于是,
无最大值.于是,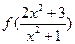 存在最大值的充要条件是
存在最大值的充要条件是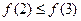 ,即
,即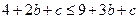 ,所以,
,所以,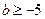 .又
.又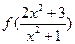 的最大值为
的最大值为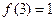 ,即
,即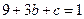 ,从而
,从而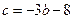 .由
.由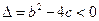 ,得
,得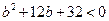 ,即
,即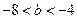 .所以
.所以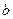 、
、 满足的条件为
满足的条件为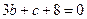 且
且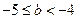 .综上:
.综上: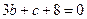 且
且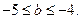
 ,
,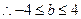 ;
;(2)须
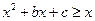 与
与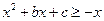 同时成立,即
同时成立,即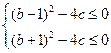 ,
,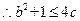 ;
;(3)因为
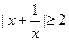 ,依题意,对一切满足
,依题意,对一切满足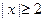 的实数
的实数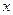 ,有
,有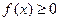 .
.①当
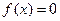 有实根时,
有实根时,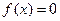 的实根在区间
的实根在区间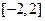 内,设
内,设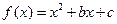 ,所以
,所以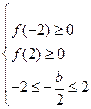 ,即
,即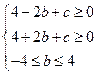 ,又
,又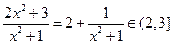 ,于是,
,于是,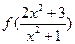 的最大值为
的最大值为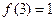 ,即
,即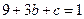 ,从而
,从而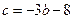 .故
.故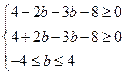 ,即
,即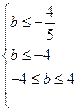 ,解得
,解得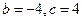 .
.②当
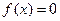 无实根时,
无实根时,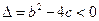 ,由二次函数性质知,
,由二次函数性质知,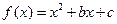 在
在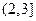 上的最大值只能在区间的端点处取得,所以,当
上的最大值只能在区间的端点处取得,所以,当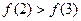 时,
时,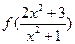 无最大值.于是,
无最大值.于是,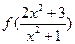 存在最大值的充要条件是
存在最大值的充要条件是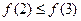 ,即
,即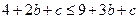 ,所以,
,所以,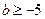 .又
.又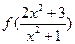 的最大值为
的最大值为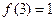 ,即
,即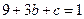 ,从而
,从而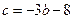 .由
.由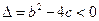 ,得
,得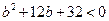 ,即
,即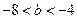 .所以
.所以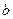 、
、 满足的条件为
满足的条件为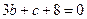 且
且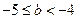 .综上:
.综上: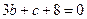 且
且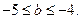

练习册系列答案
相关题目
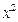 的图像大致是
的图像大致是
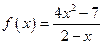 ,
,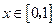 .
.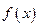 的最值;
的最值;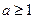 ,函数
,函数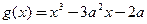 ,
,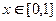 ;若对于任意
;若对于任意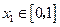 ,总存在
,总存在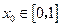 ,使得
,使得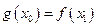 成立,求
成立,求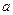 的取值范围
的取值范围
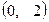 上为增函数的是 ( )
上为增函数的是 ( )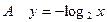
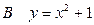
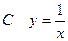

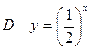
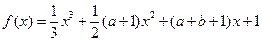 ,若方程
,若方程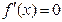 的两个实数根可以分别作为一个椭圆和双曲线的离心率,则
的两个实数根可以分别作为一个椭圆和双曲线的离心率,则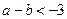
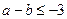
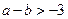
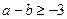
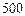
 到
到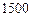
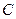 与产量
与产量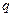 的函数关系式为
的函数关系式为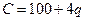
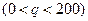 ,价格
,价格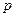 与产量
与产量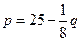 ,求产量
,求产量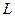 最大。
最大。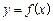 的图象如左下图所示,则函数
的图象如左下图所示,则函数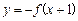 的图象大致为
的图象大致为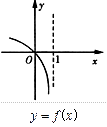

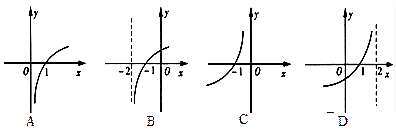

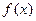 ,有下述四个命题,其中正确命题为( )
,有下述四个命题,其中正确命题为( )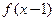 的图象关于点A(1,0)对称;
的图象关于点A(1,0)对称; 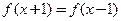 ,则
,则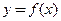 的图象关于直线
的图象关于直线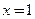 对称;
对称; 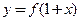 为偶函数,则
为偶函数,则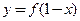 的图象关于直线
的图象关于直线