题目内容
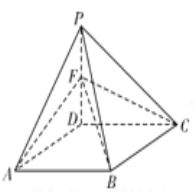
【题目】如图,在六面体![]() 中,平面
中,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() .且
.且![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析(2)![]()
【解析】
(1) 取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,通过证明
,通过证明![]() 为平行四边形,可证
为平行四边形,可证![]() ,且
,且![]() ,通过证明
,通过证明![]() 为平行四边形,可证
为平行四边形,可证![]() ,根据直线与平面平行的判定定理可证
,根据直线与平面平行的判定定理可证![]() 面
面![]() ;
;
(2) 以![]() 为坐标原点,以
为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系后,利用平面的法向量可求得结果.
轴,建立空间直角坐标系后,利用平面的法向量可求得结果.
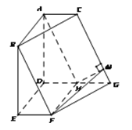
(1)取![]() 中点
中点![]() ,连接
,连接![]() 、
、![]() ,
,
如图所示:
∵![]() ,
,![]() 为
为![]() 中点,
中点,![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() 为平行四边形,
为平行四边形,
∴![]() ,且
,且![]() ,
,
∵面![]() 面
面![]() ,且面
,且面![]() 面
面![]() ,面
,面![]() 面
面![]() ,
,
∴![]() ,
,
又∵![]() ,
,![]() 且
且![]() ,
,
∴![]() ,且
,且![]() ,
,
∴![]() 为平行四边形,
为平行四边形,
∴![]() ,
,
又∵![]() 面
面![]() ,
,![]() 面
面![]() ,
,
∴![]() 面
面![]() .
.
(2)以![]() 为坐标原点,以
为坐标原点,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,以
轴,以![]() 所在直线为
所在直线为![]() 轴,建立如图所示空间直角坐标系,
轴,建立如图所示空间直角坐标系,
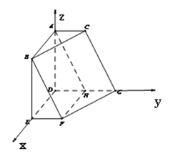
则![]() ,
,![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
∵![]() ,
,![]() ,
,
∴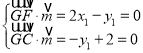 ,
,
∴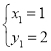 ,
,
∴![]() ,
,
同理,面![]() 的法向量
的法向量![]() ,
,
∴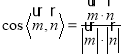
 .
.
二面角![]() 的余弦为
的余弦为![]() .
.

练习册系列答案
相关题目
【题目】某教育部门为了了解某地区高中学生校外补课的情况,随机抽取了该地区100名学生进行调查,其中女生50人,将周补课时间不低于4小时的学生称为“补课迷”.已知“补课迷”中有10名女生,右边是根据调查样本结果绘制的学生校外周补课时间的频率分布直方图(时间单位为:小时).
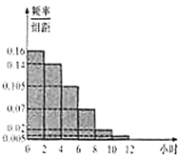
(1)根据调查样本的结果估计该地区高中学生每周课外补课的平均时间(说明:同一组中的数据用该组区间的中间值作代表);
(2)根据已知条件完成下面的![]() 列联表,根据调查资料你是否有
列联表,根据调查资料你是否有![]() 的把握认为“补课迷”与性别有关?
的把握认为“补课迷”与性别有关?
非补课迷 | 补课迷 | 合计 | |
男 | |||
女 | |||
合计 |
(3)将周补课时间不低于8小时者称为“超级补课迷”,已知调查样本中,有2名“超级补课迷”是女生,若从“超级补课迷”中任意选取3人,求至多有1名女学生的概率.
附:![]() .
.
| 0.025 | 0.010 | 0.005 | 0.001 |
| 5.024 | 6.635 | 7.879 | 10.828 |