题目内容
已知椭圆C:
+
=1(a>b>0).
(1)若椭圆的长轴长为4,离心率为
,求椭圆的标准方程;
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
| ||
|
| ||
|
(1)若椭圆的长轴长为4,离心率为
| ||
| 2 |
(2)在(1)的条件下,设过定点M(0,2)的直线l与椭圆C交于不同的两点A、B,且∠AOB为锐角(其中O为坐标原点),求直线l的斜率k的取值范围.
(1)由题意,2a=4,e=
=
,∴a=2,c=
∴b=
=1
∴椭圆C的标准方程为
+y2=1;
(2)显然直线x=0不满足条件,可设直线l:y=kx+2,A(x1,y1),B(x2,y2)
直线代入椭圆方程,消去y可得(1+4k2)x2+16kx+12=0
∵△=(16k)2-4×12×(1+4k2)>0,∴k<-
或k>
x1+x2=-
,x1x2=
∴y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=
由于∠AOB为锐角,x1x2+y1y2>0,∴
+
>0
∴2<k<2
∴直线L的斜率的取值范围是(-2,-
)∪(
,2)
| c |
| a |
| ||
| 2 |
| 3 |
∴b=
| a2-c2 |
∴椭圆C的标准方程为
| ||
| 4 |
(2)显然直线x=0不满足条件,可设直线l:y=kx+2,A(x1,y1),B(x2,y2)
直线代入椭圆方程,消去y可得(1+4k2)x2+16kx+12=0
∵△=(16k)2-4×12×(1+4k2)>0,∴k<-
| ||
| 2 |
| ||
| 2 |
x1+x2=-
| 16k |
| 1+4k2 |
| 12 |
| 1+4k2 |
∴y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=
| 4-4k2 |
| 1+4k2 |
由于∠AOB为锐角,x1x2+y1y2>0,∴
| 12 |
| 1+4k2 |
| 4-4k2 |
| 1+4k2 |
∴2<k<2
∴直线L的斜率的取值范围是(-2,-
| ||
| 2 |
| ||
| 2 |

练习册系列答案
 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目

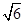 ∶3
∶3