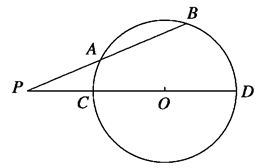
题目内容
已知a是实数,直线2x-y+5=0与直线x-y+a+4=0的交点不在椭圆x2+2y2=11上,求a的取值范围.
两条直线的交点即方程组
的解,
此时(x,y)=(a-1,2a-3).
该点不在椭圆x2+2y2=11上,
当且仅当(a-1)2+2(2a-3)2=11解得a=-2,或a=-
,
∴a≠-2且a≠-
.
∴a的取值范围是(-∞,-2)∪(-2,-
)∪(-
,+∞).
|
此时(x,y)=(a-1,2a-3).
该点不在椭圆x2+2y2=11上,
当且仅当(a-1)2+2(2a-3)2=11解得a=-2,或a=-
| 4 |
| 9 |
∴a≠-2且a≠-
| 4 |
| 9 |
∴a的取值范围是(-∞,-2)∪(-2,-
| 4 |
| 9 |
| 4 |
| 9 |

练习册系列答案
 优加精卷系列答案
优加精卷系列答案
相关题目
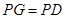 ,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.
,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F.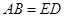 .
.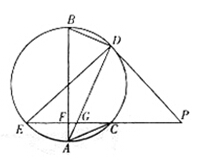
 ,PO=12,则⊙O的半径是________.
,PO=12,则⊙O的半径是________.