Question

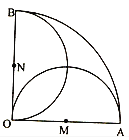
【题目】某鲜花小镇圈定一块半径为1百米的圆形荒地，准备建成各种不同鲜花景观带．为了便于游客观赏，准备修建三条道路AB，BC，CA，其中A，B，C分别为圆上的三个进出口，且A，B分别在圆心O的正东方向与正北方向上，C在圆心O南偏西某一方向上．在道路AC与BC之间修建一条直线型水渠MN种植水生观赏植物黄鸢尾（其中点M，N分别在BC和CA上，且M在圆心O的正西方向上，N在圆心O的正南方向上），并在区域MNC内种植柳叶马鞭草．

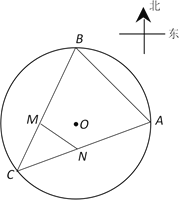
（1）求水渠MN长度的最小值；

（2）求种植柳叶马鞭草区域MNC面积的最大值（水渠宽度忽略不计）．

Answer 1

【答案】（1）百米；（2）平方米.

【解析】

（1）设，可表示出直线的方程，从而求得两点坐标，进而将表示为关于的函数，利用导数求得最值；（2）方法一：将表示为，利用将面积表示出来，利用进行换元，从而化简得：，再根据的范围求得面积最大值；方法二：利用三角形面积公式，直接用表示出，再利用换元，也可得到，从而与方法一采用相同的求最大值方法求值.

【解】（1）以圆心为原点，建立平面直角坐标系，则圆的方程为

设点，

直线的方程为，令，得

直线的方程为，令，得

所以

令，

即，

则

令，得

当时，，则单调递减；

当时，，则单调递增；

所以当时，

所以

水渠长度的最小值为百米

（2）由（1）可知，，，且

则

设，因为，所以

所以，

所以当时，

种植柳叶马鞭草区域面积的最大值为平方百米

另法：（2）因为，所以

由

所以

设，因为，所以

所以，

所以当时，

种植柳叶马鞭草区域面积的最大值为平方百米