题目内容
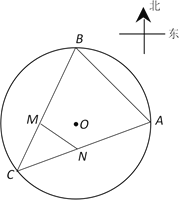
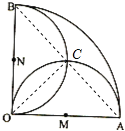
【题目】如图,在圆心角为直角的扇形OAB区域中,M、N分别为OA、OB的中点,在M、N两点处各有一个通信基站,其信号的覆盖范围分别为以OA、OB为直径的圆,在扇形OAB内随机取一点,则此点无信号的概率是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】
试题OA的中点是M,则∠CMO=90°,这样就可以求出弧OC与弦OC围成的弓形的面积,从而可求出两个圆的弧OC围成的阴影部分的面积,用扇形OAB的面积减去三角形的面积,减去加上两个弧OC围成的面积就是无信号部分的面积,最后根据几何概型的概率公式解之即可.
解:OA的中点是M,则∠CMO=90°,半径为OA=r
S扇形OAB=![]() πr2,S半圆OAC=
πr2,S半圆OAC=![]() π(
π(![]() )2=
)2=![]() πr2,
πr2,
S△OmC=![]() ×
×![]() ×
×![]() =
=![]() r2,
r2,
S弧OC=![]() S半圆OAC﹣S△ODC=
S半圆OAC﹣S△ODC=![]() πr2﹣
πr2﹣![]() r2,
r2,
两个圆的弧OC围成的阴影部分的面积为![]() πr2﹣
πr2﹣![]() r2,
r2,
图中无信号部分的面积为![]() πr2﹣
πr2﹣![]() r2﹣(
r2﹣(![]() πr2﹣
πr2﹣![]() r2)=
r2)=![]() πr2﹣
πr2﹣![]() r2,
r2,
∴无信号部分的概率是:![]() .
.
故选:B.

练习册系列答案
 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案
相关题目