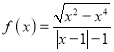题目内容
【题目】如图,在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() .
.
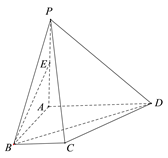
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
(i)过点![]() 作一直线
作一直线![]() 与
与![]() 平行,在图中画出直线
平行,在图中画出直线![]() 并说明理由;
并说明理由;
(ii)求平面![]() 将三棱锥
将三棱锥![]() 分成的两部分体积的比.
分成的两部分体积的比.
【答案】(1)见解析;(2)见解析,![]()
【解析】分析: (1) 取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,先证明
,先证明![]() 面
面![]() ,再证明
,再证明![]() .(2) (i)取
.(2) (i)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ,
,![]() 即为所作直线
即为所作直线![]() ,证明四边形
,证明四边形![]() 为平行四边形即得证. (ii)先分别计算出两部分的体积,再求它们的比.
为平行四边形即得证. (ii)先分别计算出两部分的体积,再求它们的比.
详解:(1)证明:(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]()

![]() ,
,![]() 为
为![]() 中点,
中点,![]()
又![]() ,
,![]() 为
为![]() 中点,
中点,![]()
又![]() ,
,![]() 面
面![]()
又![]() 面
面![]() ,
,![]()
(2)(i)取![]() 中点
中点![]() ,连接
,连接![]() ,
,![]() ,则
,则![]() ,
,![]() 即为所作直线
即为所作直线![]() ,
,
理由如下:
![]() 在
在![]() 中
中![]() 、
、![]() 分别为
分别为![]() 、
、![]() 中点
中点
![]()
![]() ,且
,且![]()
又![]() ,
,![]()
![]() 且
且![]() ,
,![]() 四边形
四边形![]() 为平行四边形.
为平行四边形.
![]()
(ii)![]() ,
,![]() ,
,![]() ,
,![]() 面
面![]()
又在![]() 中,
中,![]() ,
,![]() ,
,![]()
![]()
又![]() ,
,![]()
![]() 面
面![]()
![]()
![]()
![]() ,
, .
.

练习册系列答案
相关题目
【题目】某高中尝试进行课堂改革.现高一有![]() 两个成绩相当的班级,其中
两个成绩相当的班级,其中![]() 班级参与改革,
班级参与改革,![]() 班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过
班级没有参与改革.经过一段时间,对学生学习效果进行检测,规定成绩提高超过![]() 分的为进步明显,得到如下列联表.
分的为进步明显,得到如下列联表.
进步明显 | 进步不明显 | 合计 | |
|
|
|
|
|
|
|
|
合计 |
|
|
|
(1)是否有![]() 的把握认为成绩进步是否明显与课堂是否改革有关?
的把握认为成绩进步是否明显与课堂是否改革有关?
(2)按照分层抽样的方式从![]() 班中进步明显的学生中抽取
班中进步明显的学生中抽取![]() 人做进一步调查,然后从
人做进一步调查,然后从![]() 人中抽
人中抽![]() 人进行座谈,求这
人进行座谈,求这![]() 人来自不同班级的概率.
人来自不同班级的概率.
附: ,当
,当![]() 时,有
时,有![]() 的把握说事件
的把握说事件![]() 与
与![]() 有关.
有关.