题目内容
(本小题满分16分)
已知F是椭圆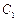 :
: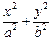 =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆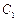 上的动点,点Q是圆
上的动点,点Q是圆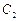 :
: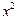 +
+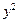 =
=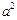 上的动点.
上的动点.
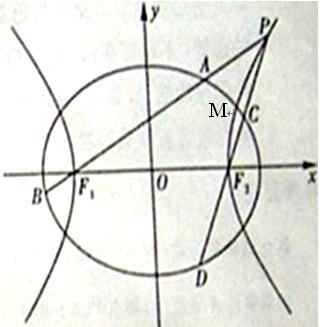
(1)试判断以PF为直径的圆与圆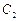 的位置关系;
的位置关系;
(2)在x轴上能否找到一定点M,使得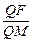 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
已知F是椭圆
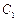 :
: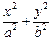 =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆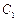 上的动点,点Q是圆
上的动点,点Q是圆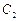 :
: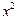 +
+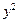 =
=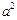 上的动点.
上的动点.(1)试判断以PF为直径的圆与圆
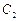 的位置关系;
的位置关系;(2)在x轴上能否找到一定点M,使得
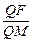 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.解析:(1)取PF的中点记为N,椭圆的左焦点记为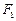 ,连结ON,则ON为
,连结ON,则ON为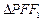 的中位线,所以ON=
的中位线,所以ON=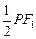 .又由椭圆的定义可知,
.又由椭圆的定义可知,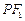 +PF=2a,从而
+PF=2a,从而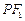 =2a-PF,故ON=
=2a-PF,故ON=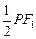 =
=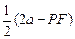 =a-
=a- .所以以PF为直径的圆与圆
.所以以PF为直径的圆与圆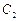 内切.
内切.
(2)设椭圆的半焦距为c,M (x,0),Q (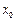 ,
, ),F (c,0),由
),F (c,0),由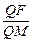 =e,得
=e,得 =
=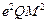 ,即
,即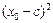 +
+ =
=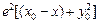 .把
.把 +
+ =
=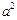 代入并化简整理,得
代入并化简整理,得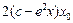 +
+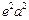 +
+ -
-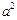 -
- =0,要此方程对任意的Q (
=0,要此方程对任意的Q (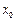 ,
, )均成立,只要
)均成立,只要 =0即可,此时x=
=0即可,此时x=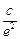 =
=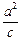 .所以x轴上存在点M,使得
.所以x轴上存在点M,使得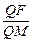 =e,M的坐标为(
=e,M的坐标为(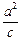 ,0).
,0).
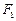 ,连结ON,则ON为
,连结ON,则ON为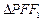 的中位线,所以ON=
的中位线,所以ON=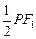 .又由椭圆的定义可知,
.又由椭圆的定义可知,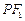 +PF=2a,从而
+PF=2a,从而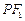 =2a-PF,故ON=
=2a-PF,故ON=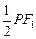 =
=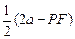 =a-
=a- .所以以PF为直径的圆与圆
.所以以PF为直径的圆与圆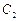 内切.
内切.(2)设椭圆的半焦距为c,M (x,0),Q (
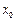 ,
, ),F (c,0),由
),F (c,0),由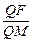 =e,得
=e,得 =
=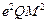 ,即
,即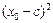 +
+ =
=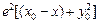 .把
.把 +
+ =
=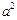 代入并化简整理,得
代入并化简整理,得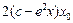 +
+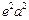 +
+ -
-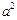 -
- =0,要此方程对任意的Q (
=0,要此方程对任意的Q (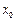 ,
, )均成立,只要
)均成立,只要 =0即可,此时x=
=0即可,此时x=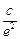 =
=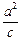 .所以x轴上存在点M,使得
.所以x轴上存在点M,使得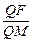 =e,M的坐标为(
=e,M的坐标为(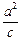 ,0).
,0).略

练习册系列答案
相关题目
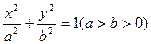 的焦点分别为
的焦点分别为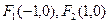 ,直线
,直线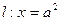 交
交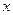 轴于点
轴于点 ,且
,且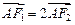 .
.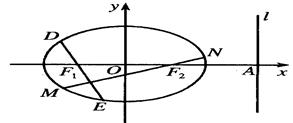
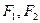 分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形
分别作互相垂直的两直线与椭圆分别交于D、E、M、N四点(如图所示),试求四边形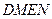 面积的最大值和最小值.
面积的最大值和最小值.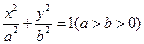 与一等轴双曲线相交,
与一等轴双曲线相交,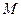 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点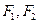 ,双曲线的焦点是椭圆的顶点
,双曲线的焦点是椭圆的顶点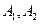 ,
,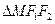 的周长为
的周长为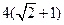 .设
.设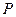 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线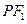 和
和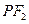 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.
 、
、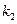 ,证明
,证明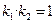 ;
;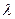 ,使得
,使得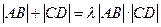 恒成立?若存在,求
恒成立?若存在,求 中,已知椭圆
中,已知椭圆 .如图所示,斜率为
.如图所示,斜率为 且不过原点的直线
且不过原点的直线 交椭圆
交椭圆 于
于 ,
, 两点,线段
两点,线段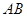 的中点为
的中点为 ,射线
,射线 交椭圆
交椭圆 ,交直线
,交直线 于点
于点 .
. 的最小值;
的最小值;
 ?
? ,(i)求证:直线
,(i)求证:直线 轴对称?若能,求出此时
轴对称?若能,求出此时 的外接圆方程;若不能,请说明理由.
的外接圆方程;若不能,请说明理由.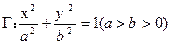 的左、右焦点为
的左、右焦点为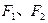 ,过点
,过点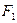 斜率为正数的直线交
斜率为正数的直线交 两点,且
两点,且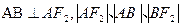 成等差数列。
成等差数列。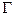 的离心率;
的离心率; 的离心率为
的离心率为 ,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为
,且两个焦点和短轴的一个端点是一个等腰三角形的顶点.斜率为 的直线
的直线 过椭圆的上焦点且与椭圆相交于
过椭圆的上焦点且与椭圆相交于 ,
, 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 轴相交于点
轴相交于点 .
. 的取值范围;
的取值范围; 的面积,并求面积的最大值.
的面积,并求面积的最大值.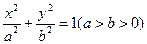 的左焦点为
的左焦点为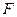 (-1,0),离心率为
(-1,0),离心率为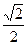 ,过点
,过点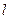 与椭圆C交于
与椭圆C交于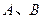 两点.
两点. 轴交于点G,求点G横坐标的取值范围.
轴交于点G,求点G横坐标的取值范围. ,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于
,P是⊙B上的动点,直线BP与线段AP的垂直平分线交于 点Q,则点Q(x,y)所满足的轨迹方程为 ( ▲ )
点Q,则点Q(x,y)所满足的轨迹方程为 ( ▲ )



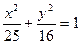 的焦点为F1,F
的焦点为F1,F 2,P为椭圆上一点,若
2,P为椭圆上一点,若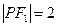 ,则
,则