题目内容
在平面直角坐标系 中,已知椭圆
中,已知椭圆 .如图所示,斜率为
.如图所示,斜率为 且不过原点的直线
且不过原点的直线 交椭圆
交椭圆 于
于 ,
, 两点,线段
两点,线段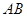 的中点为
的中点为 ,射线
,射线 交椭圆
交椭圆 于点
于点 ,交直线
,交直线 于点
于点 .
.
(Ⅰ)求 的最小值;
的最小值;
(Ⅱ)若 ?
? ,(i)求证:直线
,(i)求证:直线 过定点;
过定点;
(ii)试问点 ,
, 能否关于
能否关于 轴对称?若能,求出此时
轴对称?若能,求出此时 的外接圆方程;若不能,请说明理由.
的外接圆方程;若不能,请说明理由.
 中,已知椭圆
中,已知椭圆 .如图所示,斜率为
.如图所示,斜率为 且不过原点的直线
且不过原点的直线 交椭圆
交椭圆 于
于 ,
, 两点,线段
两点,线段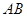 的中点为
的中点为 ,射线
,射线 交椭圆
交椭圆 于点
于点 ,交直线
,交直线 于点
于点 .
.(Ⅰ)求
 的最小值;
的最小值;
(Ⅱ)若
 ?
? ,(i)求证:直线
,(i)求证:直线 过定点;
过定点;(ii)试问点
 ,
, 能否关于
能否关于 轴对称?若能,求出此时
轴对称?若能,求出此时 的外接圆方程;若不能,请说明理由.
的外接圆方程;若不能,请说明理由.(1)2 (2)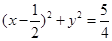
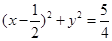
(Ⅰ)由题意:设直线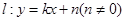 ,
,
由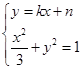 消y得:
消y得: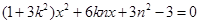 ,设A
,设A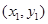 、B
、B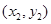 ,AB的中点E
,AB的中点E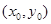 ,则由韦达定理得:
,则由韦达定理得: 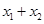 =
=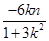 ,即
,即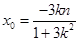 ,
,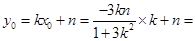
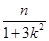 ,所以中点E的坐标为E
,所以中点E的坐标为E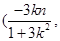
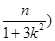 ,因为O、E、D三点在同一直线上,所以
,因为O、E、D三点在同一直线上,所以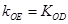 ,即
,即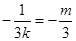 ,解得
,解得
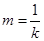 ,所以
,所以 =
=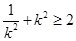 ,当且仅当
,当且仅当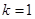 时取等号,即
时取等号,即 的最小值为2.
的最小值为2.
(Ⅱ)(i)证明:由题意知:n>0,因为直线OD的方程为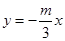 ,所以由
,所以由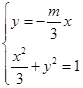 得交点G的纵坐标为
得交点G的纵坐标为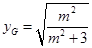 ,又因为
,又因为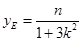 ,
,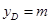 ,且
,且 ?
? ,所以
,所以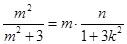 ,又由(Ⅰ)知:
,又由(Ⅰ)知: 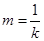 ,所以解得
,所以解得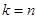 ,所以直线
,所以直线 的方程为
的方程为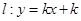 ,即有
,即有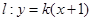 ,令
,令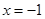 得,y=0,与实数k无关,所以直线
得,y=0,与实数k无关,所以直线 过定点(-1,0).
过定点(-1,0).
(ii)假设点 ,
, 关于
关于 轴对称,则有
轴对称,则有 的外接圆的圆心在x轴上,又在线段AB的中垂线上,
的外接圆的圆心在x轴上,又在线段AB的中垂线上,
由(i)知点G(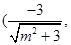
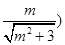 ,所
,所 以点B(
以点B(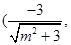
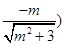 ,又因为直线
,又因为直线 过定点(-1,0),所以直线
过定点(-1,0),所以直线 的斜率为
的斜率为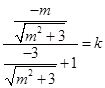 ,又因为
,又因为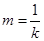 ,所以解得
,所以解得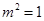 或6,又因为
或6,又因为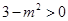 ,所以
,所以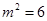 舍去,即
舍去,即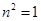 ,此时k=1
,此时k=1 ,m=1,E
,m=1,E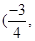
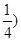 ,AB的中垂线为2x+2y+1=0,圆心坐标为
,AB的中垂线为2x+2y+1=0,圆心坐标为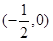 ,G(
,G(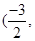
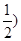 ,圆半径为
,圆半径为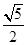 ,圆的方程为
,圆的方程为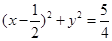 .综上所述, 点
.综上所述, 点 ,
, 关于
关于 轴对称,此时
轴对称,此时 的外接圆的方程为
的外接圆的方程为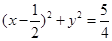 .
.
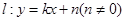 ,
,由
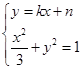 消y得:
消y得: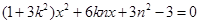 ,设A
,设A 、B
、B ,AB的中点E
,AB的中点E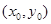 ,则由韦达定理得:
,则由韦达定理得: 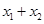 =
=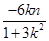 ,即
,即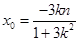 ,
,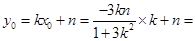
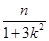 ,所以中点E的坐标为E
,所以中点E的坐标为E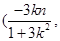
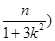 ,因为O、E、D三点在同一直线上,所以
,因为O、E、D三点在同一直线上,所以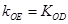 ,即
,即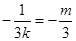 ,解得
,解得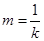 ,所以
,所以 =
=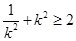 ,当且仅当
,当且仅当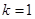 时取等号,即
时取等号,即 的最小值为2.
的最小值为2.(Ⅱ)(i)证明:由题意知:n>0,因为直线OD的方程为
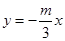 ,所以由
,所以由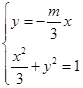 得交点G的纵坐标为
得交点G的纵坐标为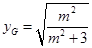 ,又因为
,又因为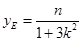 ,
,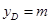 ,且
,且 ?
? ,所以
,所以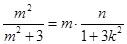 ,又由(Ⅰ)知:
,又由(Ⅰ)知: 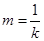 ,所以解得
,所以解得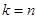 ,所以直线
,所以直线 的方程为
的方程为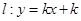 ,即有
,即有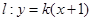 ,令
,令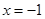 得,y=0,与实数k无关,所以直线
得,y=0,与实数k无关,所以直线 过定点(-1,0).
过定点(-1,0).(ii)假设点
 ,
, 关于
关于 轴对称,则有
轴对称,则有 的外接圆的圆心在x轴上,又在线段AB的中垂线上,
的外接圆的圆心在x轴上,又在线段AB的中垂线上,由(i)知点G(
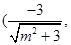
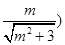 ,所
,所 以点B(
以点B(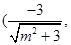
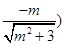 ,又因为直线
,又因为直线 过定点(-1,0),所以直线
过定点(-1,0),所以直线 的斜率为
的斜率为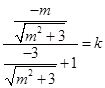 ,又因为
,又因为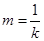 ,所以解得
,所以解得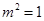 或6,又因为
或6,又因为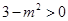 ,所以
,所以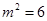 舍去,即
舍去,即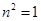 ,此时k=1
,此时k=1 ,m=1,E
,m=1,E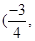
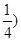 ,AB的中垂线为2x+2y+1=0,圆心坐标为
,AB的中垂线为2x+2y+1=0,圆心坐标为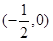 ,G(
,G(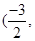
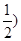 ,圆半径为
,圆半径为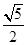 ,圆的方程为
,圆的方程为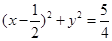 .综上所述, 点
.综上所述, 点 ,
, 关于
关于 轴对称,此时
轴对称,此时 的外接圆的方程为
的外接圆的方程为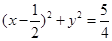 .
.
练习册系列答案
相关题目
 :
: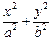 =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆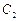 :
: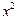 +
+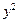 =
=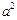 上的动点.
上的动点.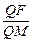 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.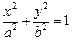 (
(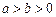 )上一点,F1,F2
)上一点,F1,F2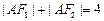 .
.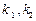 ,若存在常数
,若存在常数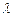 使
使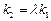 /,求直线CD的斜率.
/,求直线CD的斜率.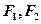 分别是椭圆
分别是椭圆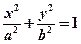
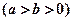 的左、右 焦点,已知点
的左、右 焦点,已知点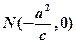 满足
满足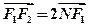 ,且
,且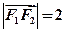 。设
。设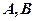 是上半椭圆上且满足
是上半椭圆上且满足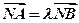 的两点。
的两点。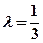 ,求直线AB的斜率。
,求直线AB的斜率。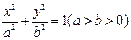 的左右焦点分别为
的左右焦点分别为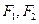 ,离心率为
,离心率为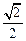 ,两焦点与上下顶点形成的菱形面积为2.
,两焦点与上下顶点形成的菱形面积为2.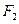 的直线
的直线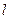 与椭圆交于A, B两点,四边形
与椭圆交于A, B两点,四边形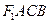 为平行四边形,
为平行四边形,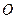 为坐标原点,且
为坐标原点,且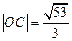 ,求直线
,求直线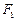 ,
,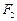 分别是椭圆
分别是椭圆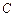 :
: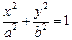 (
(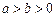 )的左、右焦点,且椭圆
)的左、右焦点,且椭圆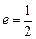 ,
,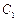 :
: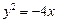 的焦点.
的焦点.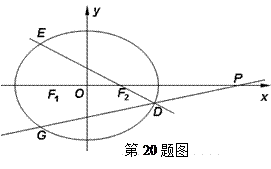
 交椭圆
交椭圆 ,
, 两点,且
两点,且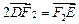 ,点
,点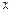 轴的对称点为
轴的对称点为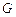 ,求直线
,求直线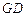 的方程.
的方程.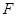 且倾斜角为
且倾斜角为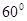 的直线交椭圆于
的直线交椭圆于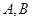 两点,若
两点,若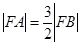 ,则椭圆的离心率等于
,则椭圆的离心率等于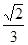
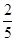
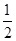
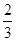
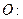
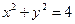 上任取一点
上任取一点 ,过点
,过点 轴的垂线段
轴的垂线段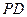 ,
,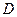 为垂足.当点
为垂足.当点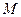 形成轨迹
形成轨迹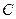 .
.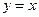 与曲线
与曲线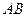 两点,
两点,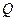 为曲线
为曲线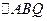 面积的最大值
面积的最大值 对于椭圆
对于椭圆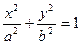 有
有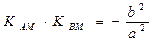 。类似地,对于双曲线
。类似地,对于双曲线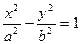 有
有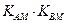 = 。
= 。