题目内容
如图,椭圆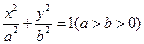 与一等轴双曲线相交,
与一等轴双曲线相交,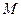 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点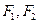 ,双曲线的焦点是椭圆的顶点
,双曲线的焦点是椭圆的顶点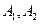 ,
,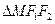 的周长为
的周长为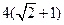 .设
.设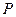 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线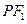 和
和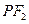 与椭圆的交点分别为
与椭圆的交点分别为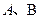 和
和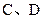 .
.
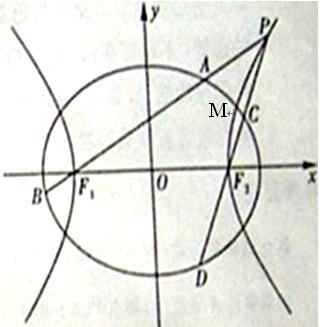
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线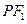 、
、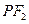 的斜率分别为
的斜率分别为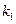 、
、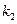 ,证明
,证明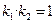 ;
;
(Ⅲ)是否存在常数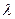 ,使得
,使得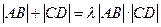 恒成立?若存在,求
恒成立?若存在,求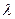 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
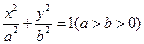 与一等轴双曲线相交,
与一等轴双曲线相交,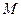 是其中一个交点,并且双曲线的顶点是该椭圆的焦点
是其中一个交点,并且双曲线的顶点是该椭圆的焦点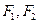 ,双曲线的焦点是椭圆的顶点
,双曲线的焦点是椭圆的顶点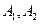 ,
,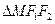 的周长为
的周长为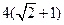 .设
.设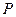 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线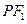 和
和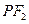 与椭圆的交点分别为
与椭圆的交点分别为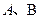 和
和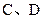 .
.
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线
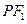 、
、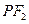 的斜率分别为
的斜率分别为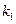 、
、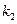 ,证明
,证明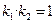 ;
;(Ⅲ)是否存在常数
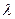 ,使得
,使得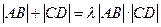 恒成立?若存在,求
恒成立?若存在,求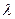 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.(Ⅰ)由题意知,双曲线的离心率为
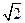 ,椭圆离心率为
,椭圆离心率为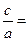
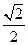 ,得
,得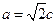 ,1分
,1分又
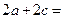
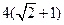 ,所以可解得
,所以可解得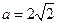 ,
,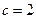 ,所以
,所以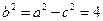 ,所以椭圆的标准方程为
,所以椭圆的标准方程为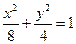 ; 4分
; 4分所以椭圆的焦点坐标为(
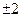 ,0),因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,所以该双曲线的标准方程为
,0),因为双曲线为等轴双曲线,且顶点是该椭圆的焦点,所以该双曲线的标准方程为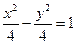 。 6分
。 6分
略

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
 :
: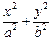 =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆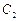 :
: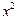 +
+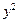 =
=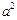 上的动点.
上的动点.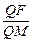 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.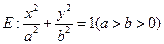 的离心率为
的离心率为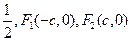 分别是左、右焦点,过F1的直线与圆
分别是左、右焦点,过F1的直线与圆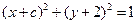 相切,且与椭圆E交于A、B两点。
相切,且与椭圆E交于A、B两点。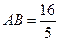 时,求椭圆E的方程;
时,求椭圆E的方程;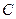 的焦点分别为
的焦点分别为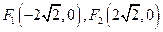 ,且过点
,且过点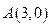 .
.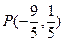 为椭圆
为椭圆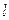 交椭圆
交椭圆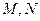 两点,且
两点,且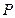 为线段
为线段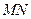 的中点,求直线
的中点,求直线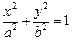 (
(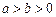 )上一点,F1,F2
)上一点,F1,F2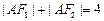 .
.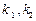 ,若存在常数
,若存在常数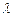 使
使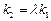 /,求直线CD的斜率.
/,求直线CD的斜率.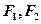 分别是椭圆
分别是椭圆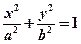
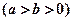 的左、右 焦点,已知点
的左、右 焦点,已知点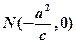 满足
满足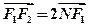 ,且
,且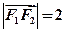 。设
。设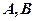 是上半椭圆上且满足
是上半椭圆上且满足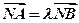 的两点。
的两点。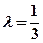 ,求直线AB的斜率。
,求直线AB的斜率。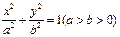 中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2
中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2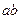 B.
B.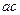 C.
C.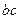 D.
D.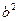
 对于椭圆
对于椭圆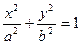 有
有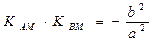 。类似地,对于双曲线
。类似地,对于双曲线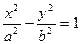 有
有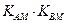 = 。
= 。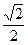
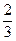 ≤e<1
≤e<1