题目内容
(本题满分12分)
已知椭圆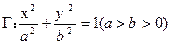 的左、右焦点为
的左、右焦点为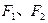 ,过点
,过点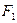 斜率为正数的直线交
斜率为正数的直线交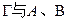 两点,且
两点,且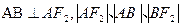 成等差数列。
成等差数列。
(Ⅰ)求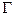 的离心率;
的离心率;
(Ⅱ)若直线y=kx(k<0)与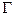 交于C、D两点,求使四边形ABCD面积S最大时k的值。
交于C、D两点,求使四边形ABCD面积S最大时k的值。
已知椭圆
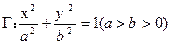 的左、右焦点为
的左、右焦点为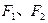 ,过点
,过点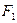 斜率为正数的直线交
斜率为正数的直线交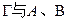 两点,且
两点,且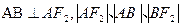 成等差数列。
成等差数列。(Ⅰ)求
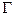 的离心率;
的离心率;(Ⅱ)若直线y=kx(k<0)与
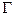 交于C、D两点,求使四边形ABCD面积S最大时k的值。
交于C、D两点,求使四边形ABCD面积S最大时k的值。(Ⅰ)根据椭圆定义及已知条件,有
|AF2|+|AB|+|BF2|=4a, ①
|AF2|+|BF2|=2|AB|, ②
|AF2|2+|AB|2=| BF2|2, ③…3分
BF2|2, ③…3分
由①、②、③,解得|AF2|=a,|AB|=a,|BF2|=a,
所以点A为短轴端点,b=c=a,Γ的离心率e==.…………………5分
(Ⅱ)由(Ⅰ),Γ的方程为x2+2y2=a2.
不妨设C(x1,y1)、D(x2,y2)(x1<x2),
则C、D坐标满足
由此得x1=-,x2=.
设C、D两点到直线AB:x-y+a=0的距离分别为d 1、d2,
1、d2,
因C、D两点在直线AB的异侧,则
d1+d2=+=
===.………………………8分
∴S=| AB|( d1+d2)=·a·=·.
AB|( d1+d2)=·a·=·.
设t=1-k,则t>1,==,
当=,即k=-时,最大,进而S有最大值.……………………12分
|AF2|+|AB|+|BF2|=4a, ①
|AF2|+|BF2|=2|AB|, ②
|AF2|2+|AB|2=|
 BF2|2, ③…3分
BF2|2, ③…3分由①、②、③,解得|AF2|=a,|AB|=a,|BF2|=a,
所以点A为短轴端点,b=c=a,Γ的离心率e==.…………………5分
(Ⅱ)由(Ⅰ),Γ的方程为x2+2y2=a2.
不妨设C(x1,y1)、D(x2,y2)(x1<x2),
则C、D坐标满足
由此得x1=-,x2=.
设C、D两点到直线AB:x-y+a=0的距离分别为d
 1、d2,
1、d2,因C、D两点在直线AB的异侧,则
d1+d2=+=
===.………………………8分
∴S=|
 AB|( d1+d2)=·a·=·.
AB|( d1+d2)=·a·=·.设t=1-k,则t>1,==,
当=,即k=-时,最大,进而S有最大值.……………………12分
略

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
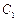 :
: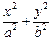 =1的右焦点,点P是椭圆
=1的右焦点,点P是椭圆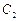 :
: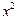 +
+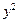 =
=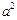 上的动点.
上的动点.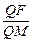 =e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.
=e (e为椭圆的离心率)?若存在,求出点M的坐标;若不存在,请说明理由.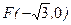 ,且过
,且过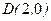 ,设点
,设点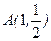 .
.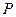 是椭圆上的动点,求线段
是椭圆上的动点,求线段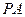 中点
中点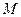 的轨迹方程;
的轨迹方程;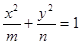 的离心率为_______________
的离心率为_______________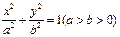 中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2
中心的直线与椭圆交于A、B两点,右焦点为F2,则△ABF2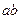 B.
B.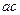 C.
C.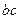 D.
D.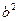
 对于椭圆
对于椭圆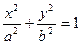 有
有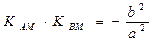 。类似地,对于双曲线
。类似地,对于双曲线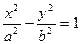 有
有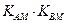 = 。
= 。




 :
: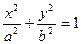 ,以抛物线
,以抛物线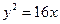 的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为
的焦点为椭圆的一个焦点,且短轴一个端点与两个焦点可组成一个等边三角形,则椭圆C的离心率为  A.
A. B.
B. 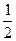 C.
C. 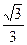 D.
D. 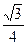
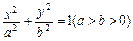 短轴端点为A,B.点P是椭圆上除A,B外任意一点,则直线PA,PB的斜率之积为 .
短轴端点为A,B.点P是椭圆上除A,B外任意一点,则直线PA,PB的斜率之积为 .